Find the feasible solution of linear inequations by graphically
The correct Answer is:z has maximum value 37 when x=4,y=5
To find the feasible solution of the linear inequalities 2x+3y≤12, 2x+y≤8, x≥0, and y≥0 graphically, follow these steps:
Step 1: Graph the first inequality 2x+3y≤12
1. Find the intercepts:
- Set x=0:
2(0)+3y=12⟹3y=12⟹y=4(Point: (0, 4))
- Set y=0:
2x+3(0)=12⟹2x=12⟹x=6(Point: (6, 0))
2. Draw the line:
- Plot the points (0, 4) and (6, 0) on the graph.
- Draw a line through these points. Since the inequality is less than or equal to, shade below the line.
Step 2: Graph the second inequality 2x+y≤8
1. Find the intercepts:
- Set x=0:
2(0)+y=8⟹y=8(Point: (0, 8))
- Set y=0:
2x+0=8⟹2x=8⟹x=4(Point: (4, 0))
2. Draw the line:
- Plot the points (0, 8) and (4, 0) on the graph.
- Draw a line through these points. Since the inequality is less than or equal to, shade below the line.
Step 3: Identify the feasible region
1. Consider the constraints x≥0 and y≥0:
- This restricts the feasible region to the first quadrant (where both x and y are non-negative).
2. Find the intersection of the shaded areas:
- The feasible solution is the area where the shaded regions from both inequalities overlap, bounded by the axes.
Step 4: Identify the vertices of the feasible region
1. Vertices:
- The points of intersection of the lines and the axes will give the vertices of the feasible region.
- The vertices can be found at:
- (0, 0) (origin)
- (0, 4) (from the first inequality)
- (4, 0) (from the second inequality)
- The intersection of the two lines can also be found by solving the equations:
2x+3y=12and2x+y=8
Subtract the second equation from the first:
2x+3y−(2x+y)=12−8⟹2y=4⟹y=2
Substitute y=2 back into 2x+y=8:
2x+2=8⟹2x=6⟹x=3
So, the intersection point is (3, 2).
Step 5: Conclusion
The feasible solution region is a quadrilateral formed by the points (0, 0), (0, 4), (4, 0), and (3, 2).
- Set x=0:
2(0)+3y=12⟹3y=12⟹y=4(Point: (0, 4))
- Set y=0:
2x+3(0)=12⟹2x=12⟹x=6(Point: (6, 0))
- Plot the points (0, 4) and (6, 0) on the graph.
- Draw a line through these points. Since the inequality is less than or equal to, shade below the line.
- Set x=0:
2(0)+y=8⟹y=8(Point: (0, 8))
- Set y=0:
2x+0=8⟹2x=8⟹x=4(Point: (4, 0))
- Plot the points (0, 8) and (4, 0) on the graph.
- Draw a line through these points. Since the inequality is less than or equal to, shade below the line.
- This restricts the feasible region to the first quadrant (where both x and y are non-negative).
- The feasible solution is the area where the shaded regions from both inequalities overlap, bounded by the axes.
- The points of intersection of the lines and the axes will give the vertices of the feasible region.
- The vertices can be found at:
- (0, 0) (origin)
- (0, 4) (from the first inequality)
- (4, 0) (from the second inequality)
- The intersection of the two lines can also be found by solving the equations:
2x+3y=12and2x+y=8
Subtract the second equation from the first:
2x+3y−(2x+y)=12−8⟹2y=4⟹y=2
Substitute y=2 back into 2x+y=8:
2x+2=8⟹2x=6⟹x=3
So, the intersection point is (3, 2).
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - DIFFERENTIATION
42 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - APPLICATIONS OF DERIVATIVE
44 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - LINE AND PLANE
40 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
The feasible region of the system of linear inequations x+2y≤120,x+y≥60,x−2y≥0,x,y≥0:
Ais bounded and lies in first quadrant .Bis unbounded and lies in first quadrant.Cdoes in first quadrant .Ddoes not exist.The solution set of linear constraints x−2y≥0,2x−y≤−2 and x,y≥0 is
A(−43,−23)B(1,1)C(0,23)D(0,2)The graphical solution of linear inequalities x+y≥5 and x−y≤3,
A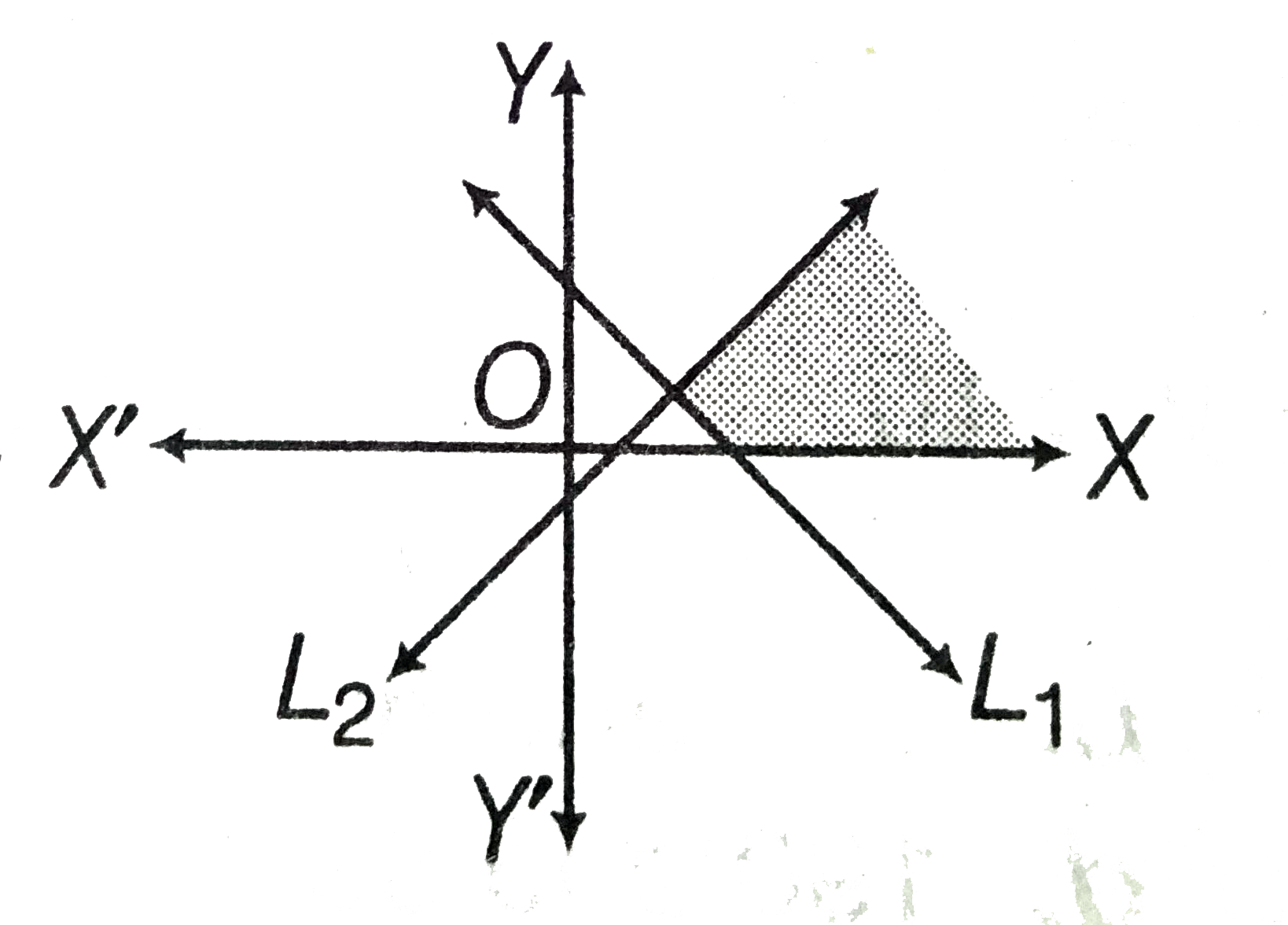 B
B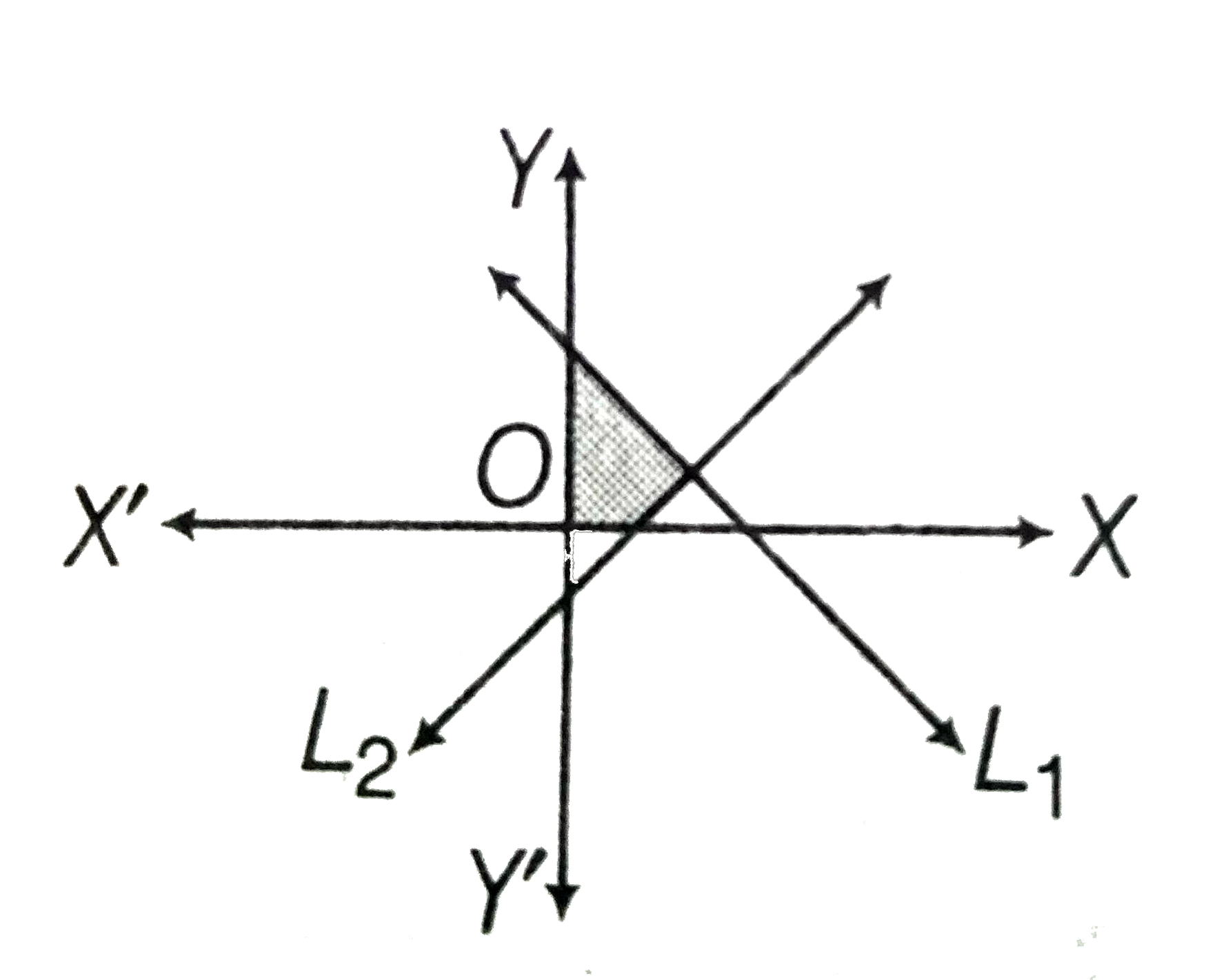 C
C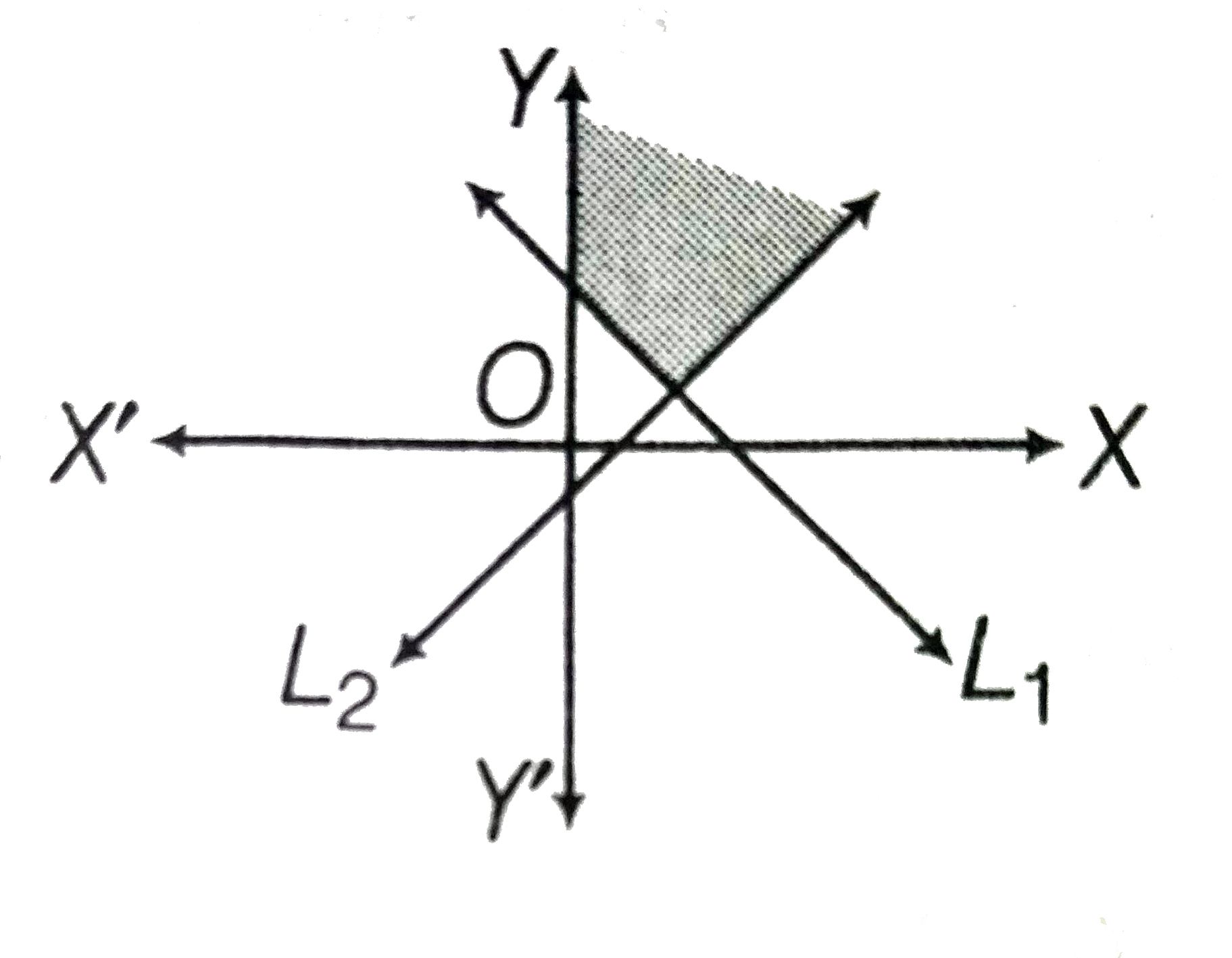 D
D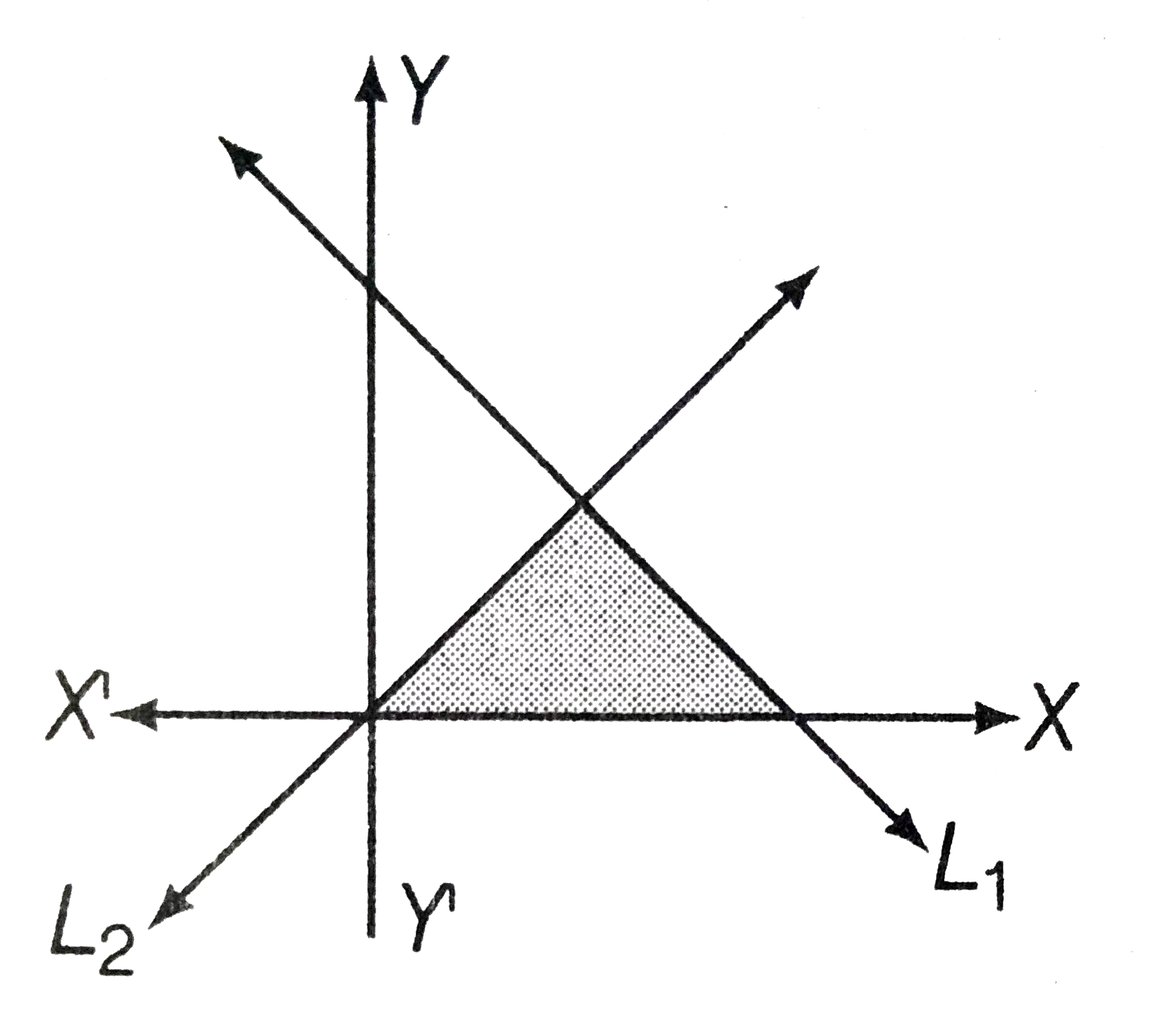
Find the graphical solutions for the system of linear inequations 2x+y≤2,x−y≤1
View SolutionThe corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
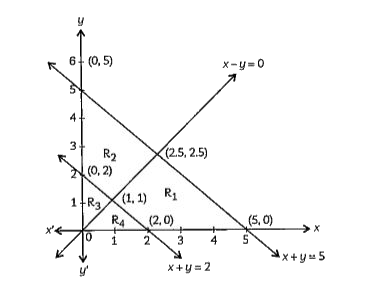
View SolutionIf the feasible region is bounded by the inequations 2x+3y≤12,2x+y≤8,0≤x,0≤y then point (5,4) is ________ of the feasible region.
View SolutionThe vertex of the linear inequalities 2x+3y≤6,x+4y≤4,x≥0,y≥0 is
View SolutionThe graphical solution of the inequalities x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0 is
View Solution
