Find the linear inequations for which the shaded area in fig. 15.41 is the solution set. Draw the diagram of the solution set of the linear inequations.
To find the linear inequalities corresponding to the shaded area in the given figure (15.41), we will analyze the lines represented in the figure and determine the inequalities based on the position of the origin (0,0) relative to these lines.
1. Identify the Lines:
We have four lines based on the video transcript:
- Line 1: −3x+2y=3
- Line 2: 2x+3y=6
- Line 3: x−2y=3
- Line 4: 4x+6y=24
2. Determine Inequalities for Each Line:
We will check whether the origin (0,0) satisfies each equation and determine the direction of the inequality.
- For Line 1:
−3(0)+2(0)=3⟹0=3 (False)
Since the origin does not satisfy the equation, we take the opposite inequality:
−3x+2y>3(or)2y>3+3x(or)y>3+3x2
- For Line 2:
2(0)+3(0)=6⟹0=6 (False)
Again, the origin does not satisfy the equation, so we take:
2x+3y<6(or)3y<6−2x(or)y<6−2x3
- For Line 3:
0−2(0)=3⟹0=3 (False)
The origin does not satisfy the equation, thus:
x−2y<3(or)−2y<3−x(or)y>x−32
- For Line 4:
4(0)+6(0)=24⟹0=24 (False)
The origin does not satisfy the equation, so we have:
4x+6y<24(or)6y<24−4x(or)y<24−4x6
3. Summary of the Inequalities:
The inequalities corresponding to the lines are:
- y>3+3x2 (from Line 1)
- y<6−2x3 (from Line 2)
- y>x−32 (from Line 3)
- y<24−4x6 (from Line 4)
4. Drawing the Diagram:
To draw the diagram, plot each line on a coordinate plane and shade the regions that satisfy the inequalities. The shaded area will represent the solution set of the linear inequalities.
We have four lines based on the video transcript:
- Line 1: −3x+2y=3
- Line 2: 2x+3y=6
- Line 3: x−2y=3
- Line 4: 4x+6y=24
We will check whether the origin (0,0) satisfies each equation and determine the direction of the inequality.
−3(0)+2(0)=3⟹0=3 (False)
Since the origin does not satisfy the equation, we take the opposite inequality:
−3x+2y>3(or)2y>3+3x(or)y>3+3x2
2(0)+3(0)=6⟹0=6 (False)
Again, the origin does not satisfy the equation, so we take:
2x+3y<6(or)3y<6−2x(or)y<6−2x3
0−2(0)=3⟹0=3 (False)
The origin does not satisfy the equation, thus:
x−2y<3(or)−2y<3−x(or)y>x−32
4(0)+6(0)=24⟹0=24 (False)
The origin does not satisfy the equation, so we have:
4x+6y<24(or)6y<24−4x(or)y<24−4x6
The inequalities corresponding to the lines are:
- y>3+3x2 (from Line 1)
- y<6−2x3 (from Line 2)
- y>x−32 (from Line 3)
- y<24−4x6 (from Line 4)
To draw the diagram, plot each line on a coordinate plane and shade the regions that satisfy the inequalities. The shaded area will represent the solution set of the linear inequalities.
Topper's Solved these Questions
Similar Questions
Find the linear inequations for which the shaded region in fig. 15.40 is the solution set.
View SolutionFind the linear equations for which the shaded area in Fig: 15.39 is the solution set.
View SolutionFind the linear inequations for which the shaded area in the figure given below is the solution set.
View SolutionFind the linear inequalities for which the shaded region in the given figure is the solution set.
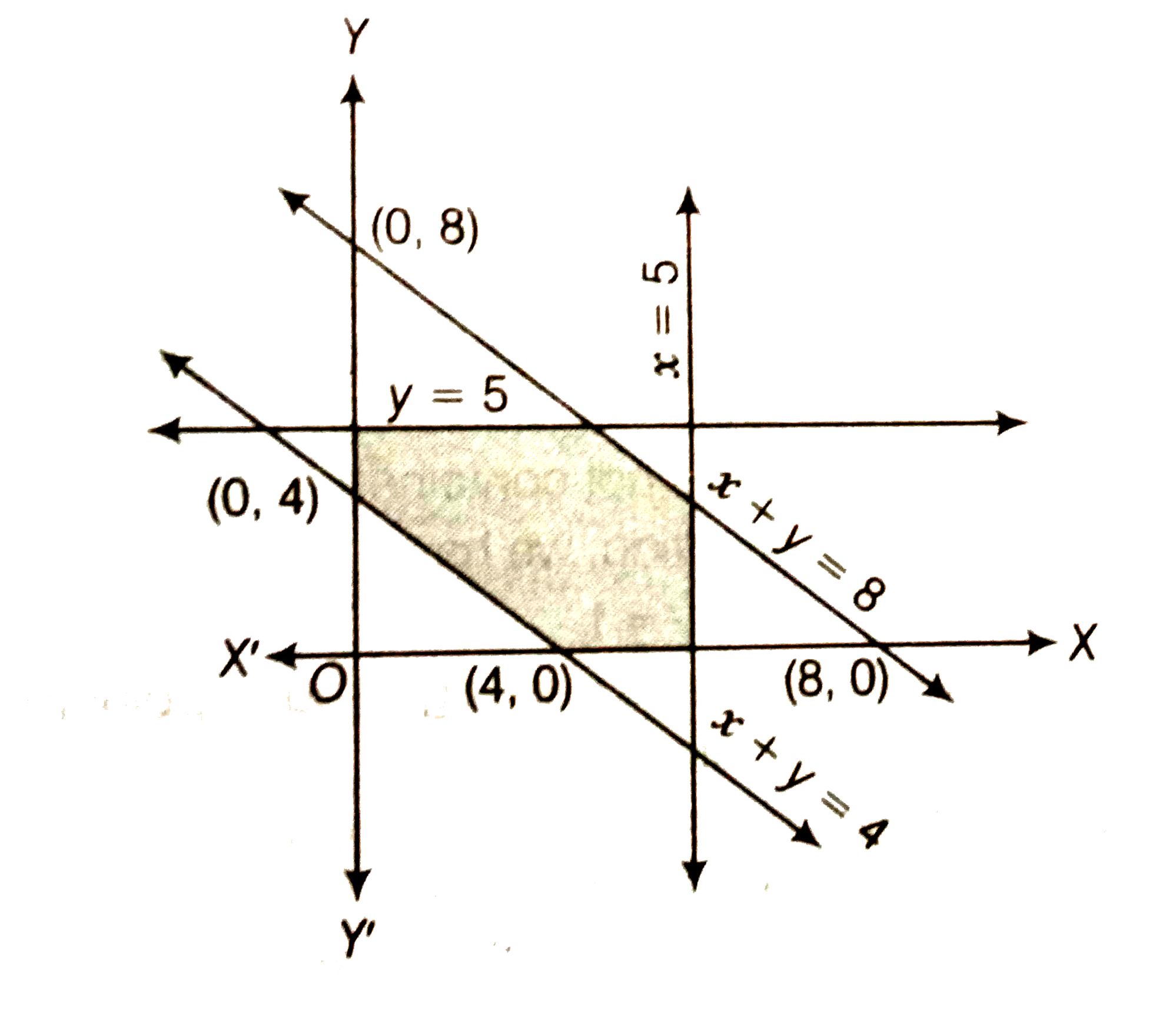
View SolutionFind the linear inequalities for which the shaded region in the given figure is the solution set.
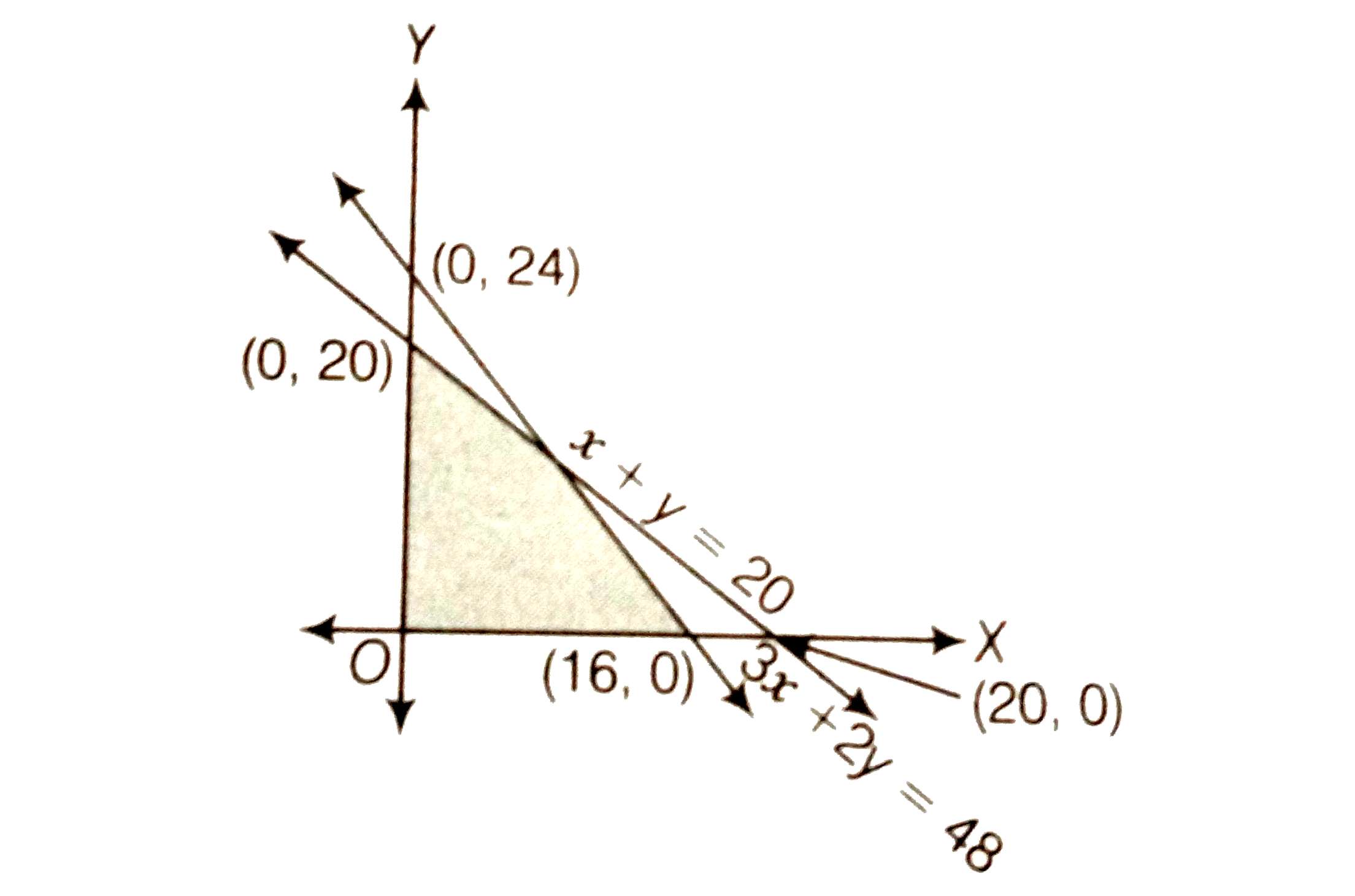
View SolutionThe solution set of the inequation 2x+y>5 is
View SolutionWrite the solution set of the inequation x+1x≥2.
View SolutionDraw the diagram f the solution set of the linear inequations 3x+4y≥12, y≥1, x≥0.
View SolutionFind the solution set of the inequality sinx>12.
View SolutionFind the solution set of the inequality sinx>12.
View Solution
