Find the mean and variance of frequency distribution given below: xi: 1≤x<3 3≤x<5 5≤x<7 7≤x<10 fi: 6 4 5 1
To find the mean and variance of the given frequency distribution, we will follow these steps:
Step 1: Create a Frequency Distribution Table
We have the following class intervals and their corresponding frequencies:
| Class Interval (x_i) | Frequency (f_i) |
|----------------------|-----------------|
| 1 < x < 3 | 6 |
| 3 < x < 5 | 4 |
| 5 < x < 7 | 5 |
| 7 < x < 10 | 1 |
Step 2: Determine the Class Marks (y_i)
The class mark (y_i) is calculated as the average of the lower and upper limits of each class interval:
- For the first interval (1 < x < 3):
y1=1+32=2
- For the second interval (3 < x < 5):
y2=3+52=4
- For the third interval (5 < x < 7):
y3=5+72=6
- For the fourth interval (7 < x < 10):
y4=7+102=8.5
Now we can add the class marks to our table:
| Class Interval (x_i) | Frequency (f_i) | Class Mark (y_i) |
|----------------------|-----------------|-------------------|
| 1 < x < 3 | 6 | 2 |
| 3 < x < 5 | 4 | 4 |
| 5 < x < 7 | 5 | 6 |
| 7 < x < 10 | 1 | 8.5 |
Step 3: Calculate f_i * y_i
Now we will calculate the product of frequency and class mark for each interval:
- f1y1=6×2=12
- f2y2=4×4=16
- f3y3=5×6=30
- f4y4=1×8.5=8.5
Adding these values gives us:
| Class Interval (x_i) | Frequency (f_i) | Class Mark (y_i) | f_i * y_i |
|----------------------|-----------------|-------------------|-----------|
| 1 < x < 3 | 6 | 2 | 12 |
| 3 < x < 5 | 4 | 4 | 16 |
| 5 < x < 7 | 5 | 6 | 30 |
| 7 < x < 10 | 1 | 8.5 | 8.5 |
Step 4: Calculate f_i * y_i^2
Next, we will calculate the square of the class marks multiplied by their respective frequencies:
- f1y21=6×22=6×4=24
- f2y22=4×42=4×16=64
- f3y23=5×62=5×36=180
- f4y24=1×8.52=1×72.25=72.25
Adding these values gives us:
| Class Interval (x_i) | Frequency (f_i) | Class Mark (y_i) | f_i * y_i | f_i * y_i^2 |
|----------------------|-----------------|-------------------|-----------|--------------|
| 1 < x < 3 | 6 | 2 | 12 | 24 |
| 3 < x < 5 | 4 | 4 | 16 | 64 |
| 5 < x < 7 | 5 | 6 | 30 | 180 |
| 7 < x < 10 | 1 | 8.5 | 8.5 | 72.25 |
Step 5: Calculate Summations
Now we will calculate the summations needed for the mean and variance:
- ∑fi=6+4+5+1=16
- ∑fiyi=12+16+30+8.5=66.5
- ∑fiy2i=24+64+180+72.25=340.25
Step 6: Calculate the Mean
The formula for the mean is:
Mean=∑fiyi∑fi=66.516=4.15625≈4.16
Step 7: Calculate the Variance
The formula for variance is:
Variance=1n∑fiy2i−(∑fiyin)2
Where n=∑fi=16.
Calculating each part:
1. 116∑fiy2i=340.2516=21.265625
2. (∑fiyin)2=(66.516)2=(4.15625)2=17.22265625
Now substituting back into the variance formula:
Variance=21.265625−17.22265625=4.04296875≈4.04
Final Answers
- Mean = 4.16
- Variance = 4.04
|----------------------|-----------------|
| 1 < x < 3 | 6 |
| 3 < x < 5 | 4 |
| 5 < x < 7 | 5 |
| 7 < x < 10 | 1 |
y1=1+32=2
y2=3+52=4
y3=5+72=6
y4=7+102=8.5
|----------------------|-----------------|-------------------|
| 1 < x < 3 | 6 | 2 |
| 3 < x < 5 | 4 | 4 |
| 5 < x < 7 | 5 | 6 |
| 7 < x < 10 | 1 | 8.5 |
- f2y2=4×4=16
- f3y3=5×6=30
- f4y4=1×8.5=8.5
|----------------------|-----------------|-------------------|-----------|
| 1 < x < 3 | 6 | 2 | 12 |
| 3 < x < 5 | 4 | 4 | 16 |
| 5 < x < 7 | 5 | 6 | 30 |
| 7 < x < 10 | 1 | 8.5 | 8.5 |
- f2y22=4×42=4×16=64
- f3y23=5×62=5×36=180
- f4y24=1×8.52=1×72.25=72.25
|----------------------|-----------------|-------------------|-----------|--------------|
| 1 < x < 3 | 6 | 2 | 12 | 24 |
| 3 < x < 5 | 4 | 4 | 16 | 64 |
| 5 < x < 7 | 5 | 6 | 30 | 180 |
| 7 < x < 10 | 1 | 8.5 | 8.5 | 72.25 |
- ∑fiyi=12+16+30+8.5=66.5
- ∑fiy2i=24+64+180+72.25=340.25
2. (∑fiyin)2=(66.516)2=(4.15625)2=17.22265625
- Variance = 4.04
Topper's Solved these Questions
Similar Questions
Find the mean and variance for the following frequency distributions in
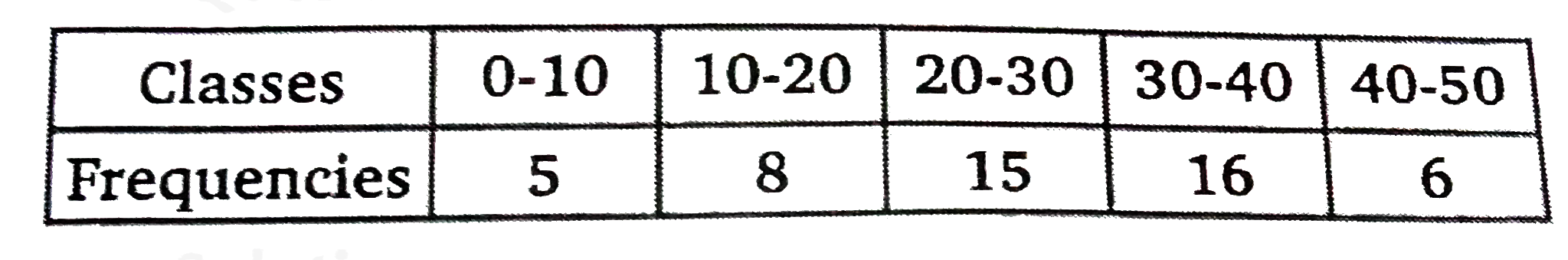 View Solution
View SolutionFind the mean and variance for the following frequency distributions in
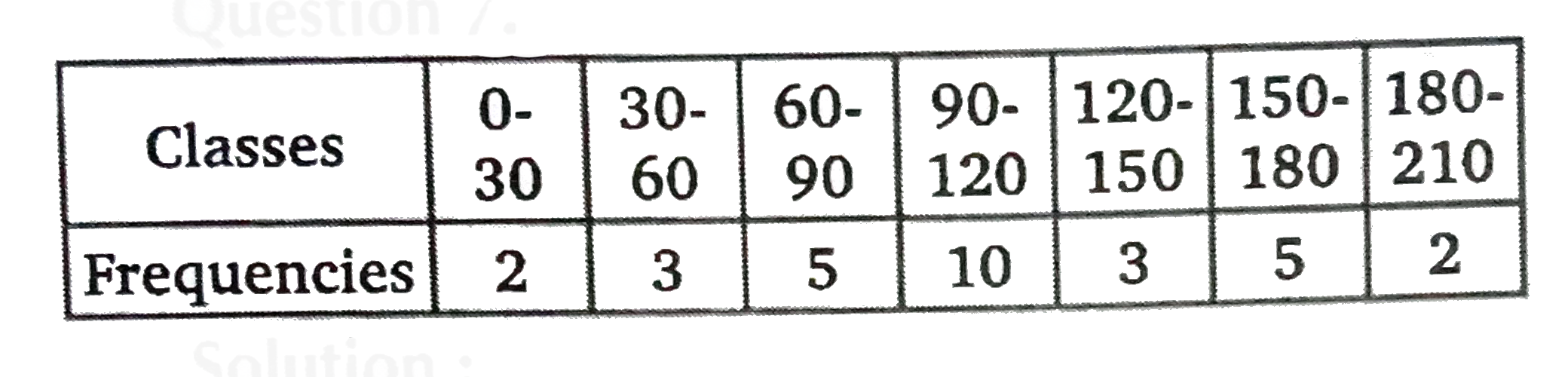 View Solution
View SolutionFind the mean for the following frequency distribution :
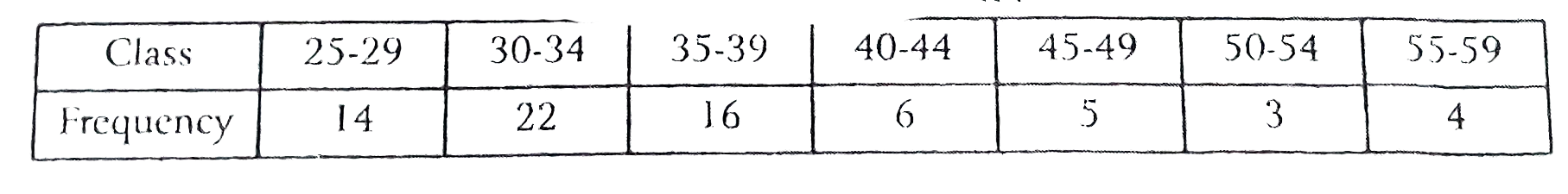 View Solution
View SolutionFind the mean and variance of Binomial Distribution if p=1/2 ,n=1
View SolutionCompute the variance of X whose distribution is given by
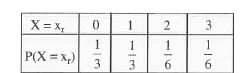 View Solution
View SolutionFind the mean and variance of the random variable X whose distribution is
 View Solution
View SolutionFind the mean of the following frequency distribution by direct method.
 View Solution
View SolutionFind the mean and standard deviation of the following frequency distribution :
 View Solution
View SolutionIf mandσ2 are the mean and variance of the random variable X, whose distribution is given by:
X=x:0123P(X=x):1312016View SolutionFind the mean and variance for the following probability distribution: ∣∣∣xi1234pi0.40.30.20.1∣∣∣
View Solution

