The measurements of the diameters (in mm) of the heads of 107 screws are given below: Diameter (in mm) 33-35 36-38 39-41 42-44 45-47 No. of screws 10 19 23 21 27. calculate mean diameter of head of screw.
To calculate the mean diameter of the heads of the screws, we will follow these steps:
Step 1: Create a Table with Class Intervals and Frequencies
We need to adjust the class intervals to make them continuous. We will subtract 0.5 from the lower limit and add 0.5 to the upper limit of each class interval.
| Class Interval (mm) | Frequency (f) |
|---------------------|---------------|
| 32.5 - 35.5 | 10 |
| 35.5 - 38.5 | 19 |
| 38.5 - 41.5 | 23 |
| 41.5 - 44.5 | 21 |
| 44.5 - 47.5 | 27 |
Step 2: Calculate the Midpoint (xi) for Each Class Interval
The midpoint (xi) is calculated as the average of the lower and upper limits of each class interval.
- For 32.5 - 35.5: x1=32.5+35.52=34.0
- For 35.5 - 38.5: x2=35.5+38.52=37.0
- For 38.5 - 41.5: x3=38.5+41.52=40.0
- For 41.5 - 44.5: x4=41.5+44.52=43.0
- For 44.5 - 47.5: x5=44.5+47.52=46.0
| Class Interval (mm) | Frequency (f) | Midpoint (xi) |
|---------------------|---------------|----------------|
| 32.5 - 35.5 | 10 | 34.0 |
| 35.5 - 38.5 | 19 | 37.0 |
| 38.5 - 41.5 | 23 | 40.0 |
| 41.5 - 44.5 | 21 | 43.0 |
| 44.5 - 47.5 | 27 | 46.0 |
Step 3: Calculate the Product of Frequency and Midpoint (f * xi)
Now we will calculate the product of frequency and midpoint for each class interval.
- For 32.5 - 35.5: f1⋅x1=10⋅34.0=340.0
- For 35.5 - 38.5: f2⋅x2=19⋅37.0=703.0
- For 38.5 - 41.5: f3⋅x3=23⋅40.0=920.0
- For 41.5 - 44.5: f4⋅x4=21⋅43.0=903.0
- For 44.5 - 47.5: f5⋅x5=27⋅46.0=1242.0
| Class Interval (mm) | Frequency (f) | Midpoint (xi) | f * xi |
|---------------------|---------------|----------------|---------|
| 32.5 - 35.5 | 10 | 34.0 | 340.0 |
| 35.5 - 38.5 | 19 | 37.0 | 703.0 |
| 38.5 - 41.5 | 23 | 40.0 | 920.0 |
| 41.5 - 44.5 | 21 | 43.0 | 903.0 |
| 44.5 - 47.5 | 27 | 46.0 | 1242.0 |
Step 4: Calculate the Sum of Frequencies and Sum of f * xi
Now we will calculate the total frequency and the total of f * xi.
- Total frequency Σf=10+19+23+21+27=100
- Total of f⋅xi Σ(f⋅x)=340+703+920+903+1242=4108
Step 5: Calculate the Mean Diameter
Finally, we can calculate the mean diameter using the formula:
Mean=Σ(f⋅x)Σf=4108100=41.08 mm
Final Answer
The mean diameter of the head of the screws is 41.08 mm.
---
We need to adjust the class intervals to make them continuous. We will subtract 0.5 from the lower limit and add 0.5 to the upper limit of each class interval.
|---------------------|---------------|
| 32.5 - 35.5 | 10 |
| 35.5 - 38.5 | 19 |
| 38.5 - 41.5 | 23 |
| 41.5 - 44.5 | 21 |
| 44.5 - 47.5 | 27 |
The midpoint (xi) is calculated as the average of the lower and upper limits of each class interval.
- For 35.5 - 38.5: x2=35.5+38.52=37.0
- For 38.5 - 41.5: x3=38.5+41.52=40.0
- For 41.5 - 44.5: x4=41.5+44.52=43.0
- For 44.5 - 47.5: x5=44.5+47.52=46.0
|---------------------|---------------|----------------|
| 32.5 - 35.5 | 10 | 34.0 |
| 35.5 - 38.5 | 19 | 37.0 |
| 38.5 - 41.5 | 23 | 40.0 |
| 41.5 - 44.5 | 21 | 43.0 |
| 44.5 - 47.5 | 27 | 46.0 |
Now we will calculate the product of frequency and midpoint for each class interval.
- For 35.5 - 38.5: f2⋅x2=19⋅37.0=703.0
- For 38.5 - 41.5: f3⋅x3=23⋅40.0=920.0
- For 41.5 - 44.5: f4⋅x4=21⋅43.0=903.0
- For 44.5 - 47.5: f5⋅x5=27⋅46.0=1242.0
|---------------------|---------------|----------------|---------|
| 32.5 - 35.5 | 10 | 34.0 | 340.0 |
| 35.5 - 38.5 | 19 | 37.0 | 703.0 |
| 38.5 - 41.5 | 23 | 40.0 | 920.0 |
| 41.5 - 44.5 | 21 | 43.0 | 903.0 |
| 44.5 - 47.5 | 27 | 46.0 | 1242.0 |
Now we will calculate the total frequency and the total of f * xi.
- Total of f⋅xi Σ(f⋅x)=340+703+920+903+1242=4108
Finally, we can calculate the mean diameter using the formula:
The mean diameter of the head of the screws is 41.08 mm.
Topper's Solved these Questions
Similar Questions
The measurements of the diameters (in mm) of the heads of 107 screws are given below: Diameter (in mm), 33-35, 36-38, 39-41, 42-44, 45-47 No. of screws, 10, 19, 23, 21, 27. Find the mean diameter.
View SolutionGiven below are the diameters of circles (in mm) drawn in a design.
Diameter33−3637−4041−4445−4849−52Number of Circles1517212225
Calculate the mean diameter of the circles, variance and standard deviation.
View SolutionThe diameter of circles (in mm) drawn in a design are given below:
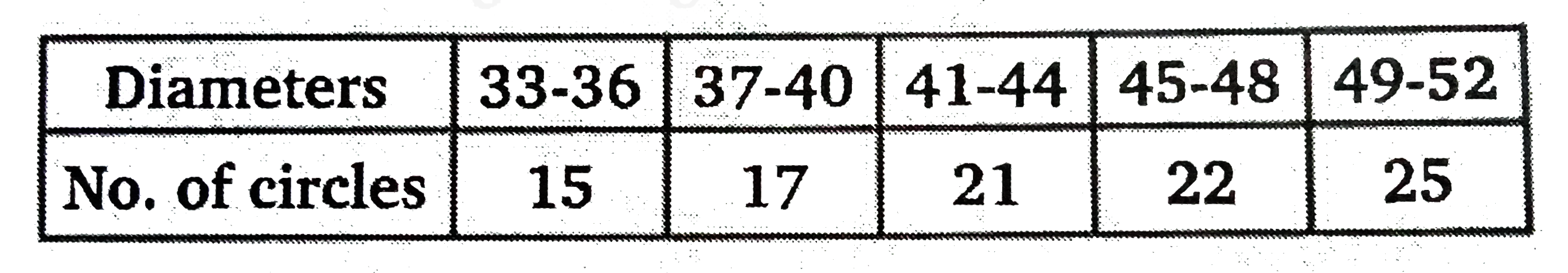
Calculate the standard deviation and mean diameter of the circles.
View SolutionCalculate the mean deviation about median age for the age distribution of 100 persons given below: Age 16-20 21-25 26-30 31-35 36-40 41-45 46-50 51-55 Number 5 6 12 14 26 12 16 9
View SolutionCalculate the mean deviation about median age for the age distribution of 100 persons given below: Age 16-20 21-25 26-30 31-35 36-40 41-45 46-50 51-55 Number 5 6 12 14 26 12 16 9
View SolutionThe pitch of a screw gauge is 1mm and its cap is divided into 100 divisions. When this screw gauge is used to measure the diameter of a wire, then main scale reading is 2mm and 58th division of circular scale coincides with the main scale. There is no zero error in the screw gage. Then the diameter of the wire is
View SolutionUsing a screw gauge the diameter was measured. The readings are given belwo: 0.39 mm, 0.38 mm, 0.39 mm, 0.41 mm, 0.38 mm, 0.37 m, 0.40 mm,0.39 mm. Calculate (i) the most accurate value of the diameter (ii) the relative error and (iii) percentage error.
View SolutionWhen a screw gauge of least count 0.01 mm is used to measure the diameter of a wire, the reading on the sleeve is found to be 1 mm and the reading on the thimble is found to be 27 divisions.What is the diameter of the wire in cm ?
View SolutionThe pitch of a screw gauge is 1mmandthereare100÷isions on the circular scale. In measuring the diameter of a sphere there are six divisions on the linear scale and forty divisions on circular scale coincide with the reference line. Find the diameter of the sphere.
View SolutionA screw gauge gives the following reading when used to mesure the diametre of a wire.
Main scale reading : 0mm
Circular scale reading : 52 divisions
Given that 1mm on main scale corresponds to 100 divisions of the circular scale. the diameter of wire from the above data is :
View Solution
