Find the mean deviation about the mean for the data :xi 10 30 50 70 90fi 4 24 28 16 8
To find the mean deviation about the mean for the given data, we will follow these steps:
Step 1: Calculate the Mean (x̄)
We need to calculate the mean using the formula:
xˉ=Σ(fi⋅xi)Σfi
Where:
- xi are the values: 10, 30, 50, 70, 90
- fi are the frequencies: 4, 24, 28, 16, 8
First, we calculate fi⋅xi:
f1⋅x1=4⋅10=40f2⋅x2=24⋅30=720f3⋅x3=28⋅50=1400f4⋅x4=16⋅70=1120f5⋅x5=8⋅90=720
Now, sum these values:
Σ(fi⋅xi)=40+720+1400+1120+720=4000
Next, calculate Σfi:
Σfi=4+24+28+16+8=80
Now, substitute these into the mean formula:
xˉ=400080=50
Step 2: Calculate the Absolute Deviations
Now, we calculate the absolute deviations |xi−xˉ|:
|10−50|=40|30−50|=20|50−50|=0|70−50|=20|90−50|=40
Step 3: Calculate fi⋅|xi−xˉ|
Now, we multiply these absolute deviations by their corresponding frequencies:
f1⋅|x1−xˉ|=4⋅40=160f2⋅|x2−xˉ|=24⋅20=480f3⋅|x3−xˉ|=28⋅0=0f4⋅|x4−xˉ|=16⋅20=320f5⋅|x5−xˉ|=8⋅40=320
Now, sum these values:
Σ(fi⋅|xi−xˉ|)=160+480+0+320+320=1280
Step 4: Calculate the Mean Deviation
Finally, we calculate the mean deviation using the formula:
Mean Deviation=Σ(fi⋅|xi−xˉ|)Σfi
Substituting the values we found:
Mean Deviation=128080=16
Final Answer
The mean deviation about the mean for the given data is 16.
---
We need to calculate the mean using the formula:
- xi are the values: 10, 30, 50, 70, 90
- fi are the frequencies: 4, 24, 28, 16, 8
Now, we calculate the absolute deviations |xi−xˉ|:
Now, we multiply these absolute deviations by their corresponding frequencies:
Finally, we calculate the mean deviation using the formula:
The mean deviation about the mean for the given data is 16.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.35videos
STATISTICS
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.210videos
STATISTICS
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - SOLVED EXAMPLES18videos
STATISTICS
- BOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.57videos
SETS
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.52videos
STRAIGHT LINES
Similar Questions
Find the mean deviation about the mean for the data :
 View Solution
View SolutionFind the mean deviation about the mean for the data :xi 10 30 50 70 90fi 4 24 28 16 8
View SolutionFind the mean deviation about the mean for the data is Question:
 View Solution
View SolutionFind the mean deviation about the mean for the data is Question:
 View Solution
View SolutionFind the mean deviation about the mean for the data in Question:
 View Solution
View SolutionFind the mean deviation about the mean for the data in Question:
 View Solution
View SolutionFind the mean deviation about the mean for the following data :
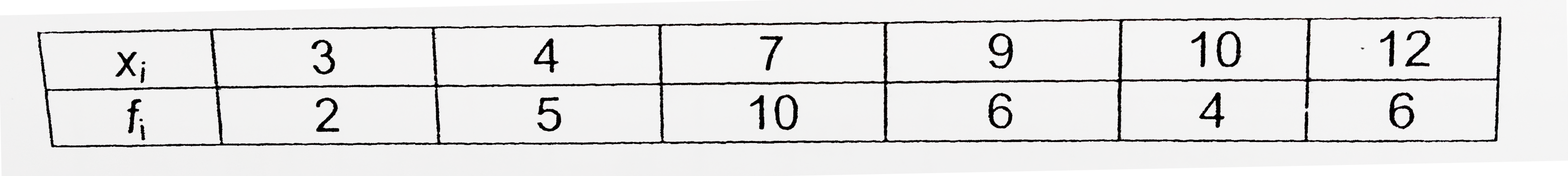 View Solution
View SolutionFind the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation about the median for the data in Question
 View Solution
View SolutionFind the mean deviation about the median for the data in Question
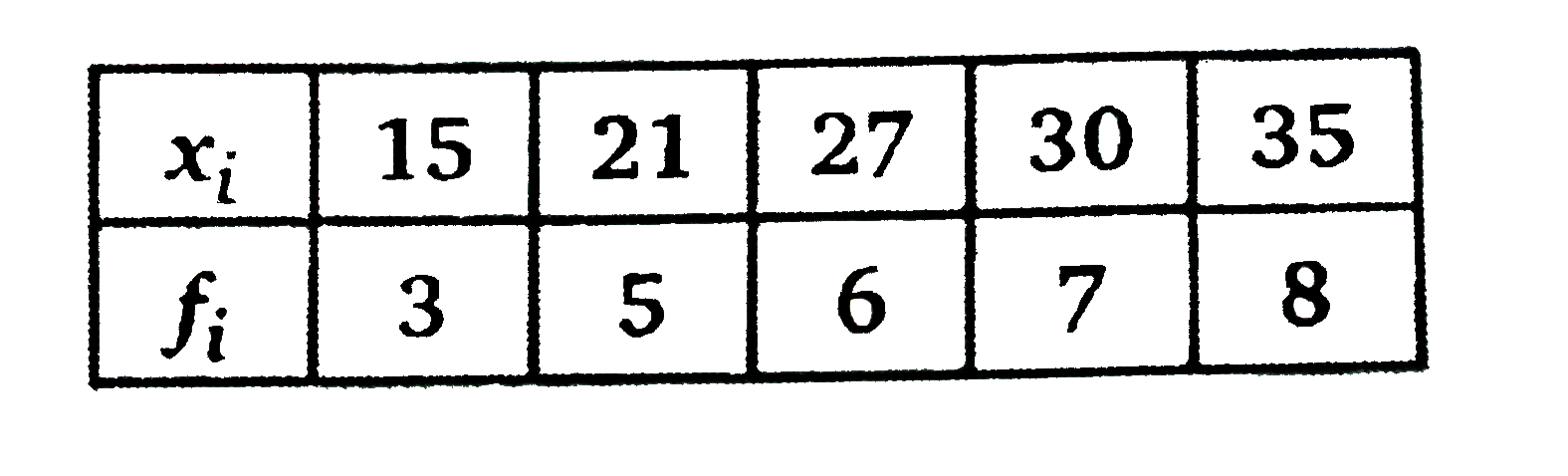 View Solution
View Solution

