Find the mean of the following frequency distribution: Classes: 0-20 20-40 40-60 60-80 80-100 Frequency: 15 18 21 29 17
To find the mean of the given frequency distribution, we will follow these steps:
Step 1: Create a table for the frequency distribution
We will list the classes and their corresponding frequencies.
| Class | Frequency (f) |
|-----------|---------------|
| 0 - 20 | 15 |
| 20 - 40 | 18 |
| 40 - 60 | 21 |
| 60 - 80 | 29 |
| 80 - 100 | 17 |
Step 2: Calculate the midpoints (x) for each class
The midpoint for each class can be calculated using the formula:
x=Lower limit+Upper limit2
Calculating midpoints:
- For the class 0-20: x1=0+202=10
- For the class 20-40: x2=20+402=30
- For the class 40-60: x3=40+602=50
- For the class 60-80: x4=60+802=70
- For the class 80-100: x5=80+1002=90
Now, we can create a new table with midpoints:
| Class | Frequency (f) | Midpoint (x) |
|-----------|---------------|---------------|
| 0 - 20 | 15 | 10 |
| 20 - 40 | 18 | 30 |
| 40 - 60 | 21 | 50 |
| 60 - 80 | 29 | 70 |
| 80 - 100 | 17 | 90 |
Step 3: Calculate f⋅x for each class
Now we will multiply the frequency by the midpoint for each class.
| Class | Frequency (f) | Midpoint (x) | f⋅x |
|-----------|---------------|---------------|------------------|
| 0 - 20 | 15 | 10 | 15⋅10=150 |
| 20 - 40 | 18 | 30 | 18⋅30=540 |
| 40 - 60 | 21 | 50 | 21⋅50=1050 |
| 60 - 80 | 29 | 70 | 29⋅70=2030 |
| 80 - 100 | 17 | 90 | 17⋅90=1530 |
Step 4: Sum up the frequencies and f⋅x
Now, we will calculate the total of frequencies and the total of f⋅x.
- Total frequency ∑f=15+18+21+29+17=100
- Total f⋅x=150+540+1050+2030+1530=4300
Step 5: Calculate the mean
The mean can be calculated using the formula:
Mean=∑(f⋅x)∑f
Substituting the values:
Mean=4300100=43
Final Answer
The mean of the given frequency distribution is 43.
---
We will list the classes and their corresponding frequencies.
|-----------|---------------|
| 0 - 20 | 15 |
| 20 - 40 | 18 |
| 40 - 60 | 21 |
| 60 - 80 | 29 |
| 80 - 100 | 17 |
The midpoint for each class can be calculated using the formula:
x=Lower limit+Upper limit2
- For the class 0-20: x1=0+202=10
- For the class 20-40: x2=20+402=30
- For the class 40-60: x3=40+602=50
- For the class 60-80: x4=60+802=70
- For the class 80-100: x5=80+1002=90
|-----------|---------------|---------------|
| 0 - 20 | 15 | 10 |
| 20 - 40 | 18 | 30 |
| 40 - 60 | 21 | 50 |
| 60 - 80 | 29 | 70 |
| 80 - 100 | 17 | 90 |
Now we will multiply the frequency by the midpoint for each class.
|-----------|---------------|---------------|------------------|
| 0 - 20 | 15 | 10 | 15⋅10=150 |
| 20 - 40 | 18 | 30 | 18⋅30=540 |
| 40 - 60 | 21 | 50 | 21⋅50=1050 |
| 60 - 80 | 29 | 70 | 29⋅70=2030 |
| 80 - 100 | 17 | 90 | 17⋅90=1530 |
Now, we will calculate the total of frequencies and the total of f⋅x.
- Total f⋅x=150+540+1050+2030+1530=4300
The mean can be calculated using the formula:
Mean=∑(f⋅x)∑f
Mean=4300100=43
The mean of the given frequency distribution is 43.
Topper's Solved these Questions
Similar Questions
Find the mean of the following frequency distributions: Class interval: 0-10 10-20 20-30 30-40 40-50 Frequency: 9 12 15 10 14
View SolutionFind the mean of the following frequency distribution: Class-interval: 0-10 10-20 20-30 30-40 40-50 No. of workers f: 7 10 15 8 10
View SolutionFind the mode from the following frequency distribution: Class 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Frequency 8 10 10 16 12 6 7
View SolutionThe mean of the following frequency distribution is 50. Find the value of p. Classes 0-20 20-40 40-60 60-80 80-100 Frequency 17 28 32 p 19
View SolutionFind the mean of the following frequency distribution using step-deviation method. Class 0-10 10-20 20-30 30-40 40-50 Frequency 7 10 15 8 10
View SolutionFind the mean of the following frequency distribution, using step-deviation method: Class 0-10 10-20 20-30 30-40 40-50 Frequency 7 12 13 10 8
View SolutionThe mean of the following distribution is 18. Find the frequency f of the class 19−21.
View SolutionConsider the following distribution
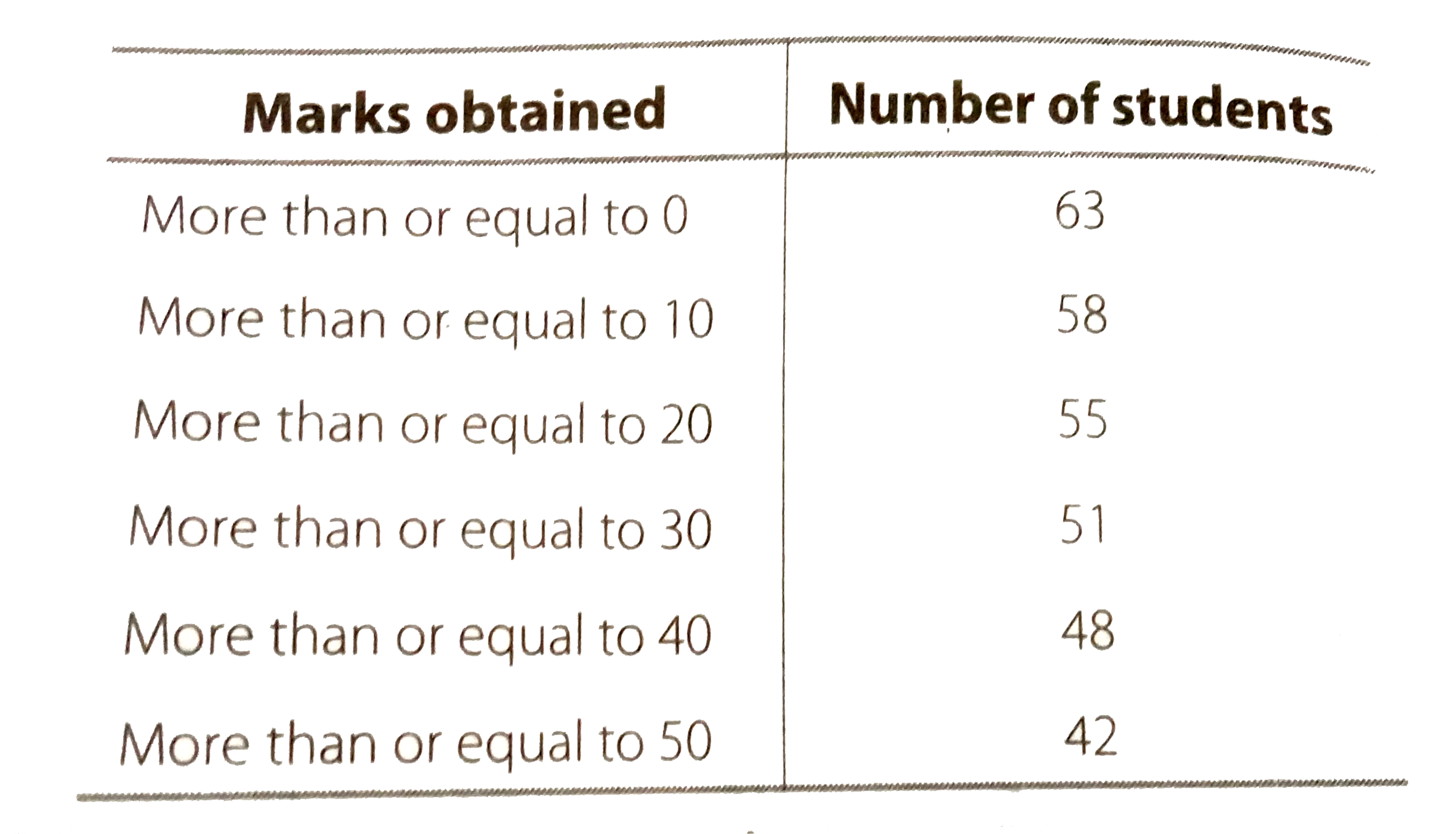
Frequency of the class 30-40 isView SolutionWrite the median class of the following distribution: Classes: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Frequency: 4 4 8 10 12 8 4
View SolutionFind the mode of the following data: Class Frequency 0-20 15 20-40 6 40-60 18 60-80 10
View Solution

