Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No. of accident (x), 0, 1 , 2 , 3, 4, 5 , Total Frequency is 200 and no. of days (f): 46 , ? , ? , 25 , 10 , 5
To find the missing frequencies in the given frequency distribution, we will follow these steps:
Step 1: Set up the frequency distribution table
We have the following data:
| No. of Accidents (x) | Frequency (f) |
|-----------------------|---------------|
| 0 | 46 |
| 1 | F1 |
| 2 | F2 |
| 3 | 25 |
| 4 | 10 |
| 5 | 5 |
| Total | 200 |
Step 2: Write the equations based on the total frequency
The total frequency is given as 200. Therefore, we can write the equation:
46+F1+F2+25+10+5=200
Calculating the known frequencies:
46+25+10+5=86
Thus, we have:
F1+F2+86=200
This simplifies to:
F1+F2=114(Equation 1)
Step 3: Calculate the weighted sum of frequencies
We need to calculate the sum of xi⋅fi:
Sum=0⋅46+1⋅F1+2⋅F2+3⋅25+4⋅10+5⋅5
Calculating the known products:
0+F1+2F2+75+40+25=F1+2F2+140
Step 4: Use the mean to set up another equation
The mean of the distribution is given as 1.46. The formula for the mean is:
Mean=∑(xi⋅fi)∑fi
Substituting the known values:
1.46=F1+2F2+140200
Multiplying both sides by 200 gives:
292=F1+2F2+140
Rearranging this gives:
F1+2F2=292−140
Thus:
F1+2F2=152(Equation 2)
Step 5: Solve the system of equations
Now we have two equations:
1. F1+F2=114
2. F1+2F2=152
We can solve these equations simultaneously. Subtract Equation 1 from Equation 2:
(F1+2F2)−(F1+F2)=152−114
This simplifies to:
F2=38
Step 6: Substitute back to find F1
Now substitute F2=38 back into Equation 1:
F1+38=114
Thus:
F1=114−38=76
Conclusion
The missing frequencies are:
- F1=76
- F2=38
Summary of the missing frequencies:
- Frequency for 1 accident (F1) = 76
- Frequency for 2 accidents (F2) = 38
---
We have the following data:
|-----------------------|---------------|
| 0 | 46 |
| 1 | F1 |
| 2 | F2 |
| 3 | 25 |
| 4 | 10 |
| 5 | 5 |
| Total | 200 |
The total frequency is given as 200. Therefore, we can write the equation:
46+F1+F2+25+10+5=200
Calculating the known frequencies:
46+25+10+5=86
Thus, we have:
F1+F2+86=200
This simplifies to:
F1+F2=114(Equation 1)
We need to calculate the sum of xi⋅fi:
Sum=0⋅46+1⋅F1+2⋅F2+3⋅25+4⋅10+5⋅5
Calculating the known products:
0+F1+2F2+75+40+25=F1+2F2+140
The mean of the distribution is given as 1.46. The formula for the mean is:
Mean=∑(xi⋅fi)∑fi
Substituting the known values:
1.46=F1+2F2+140200
Multiplying both sides by 200 gives:
292=F1+2F2+140
Rearranging this gives:
F1+2F2=292−140
Thus:
F1+2F2=152(Equation 2)
Now we have two equations:
1. F1+F2=114
2. F1+2F2=152
(F1+2F2)−(F1+F2)=152−114
This simplifies to:
F2=38
Now substitute F2=38 back into Equation 1:
F1+38=114
Thus:
F1=114−38=76
The missing frequencies are:
- F1=76
- F2=38
- Frequency for 1 accident (F1) = 76
- Frequency for 2 accidents (F2) = 38
Topper's Solved these Questions
Similar Questions
Find the mean for the following frequency distribution :
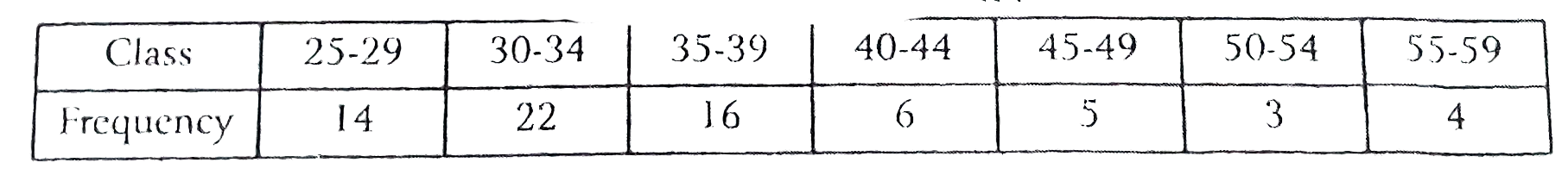 View Solution
View SolutionFind the mean and variance for the following frequency distributions in
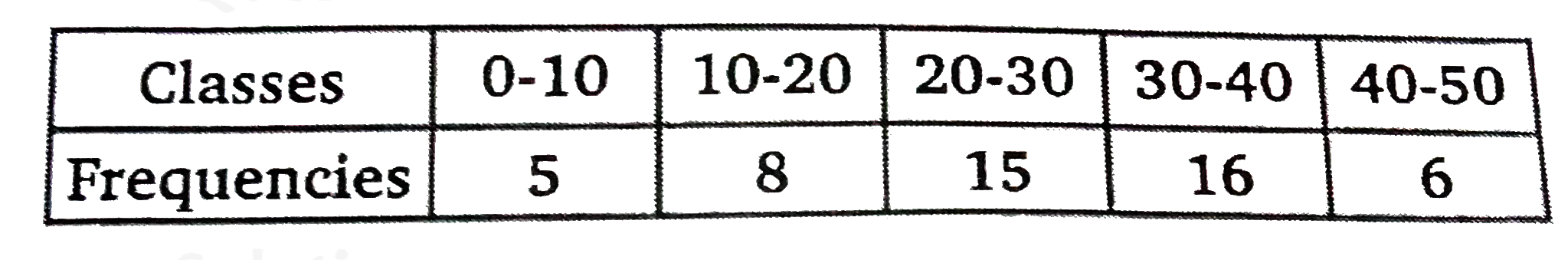 View Solution
View SolutionFind the mean and variance for the following frequency distributions in
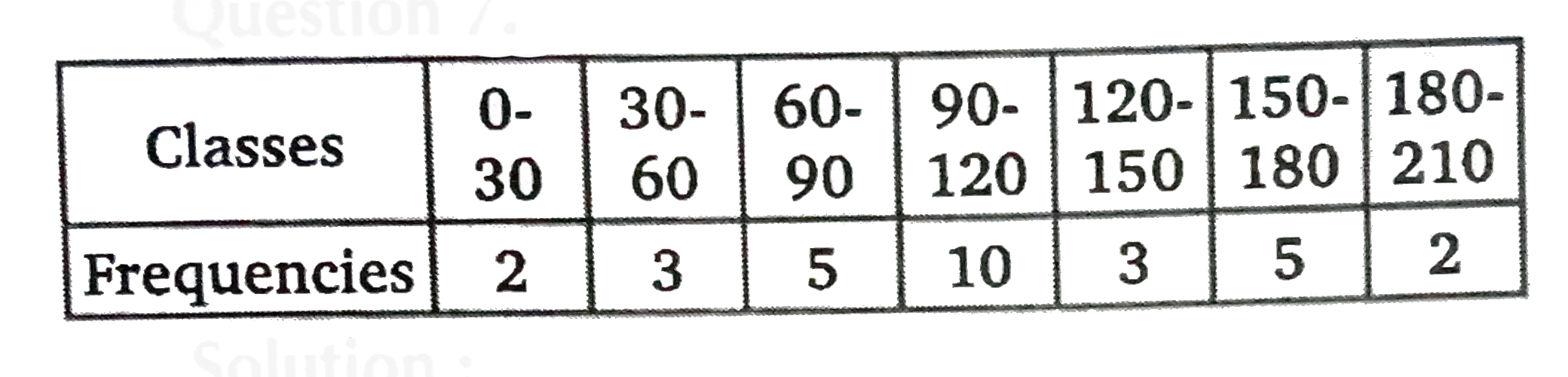 View Solution
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No. of accident (x) 0 1 2 3 4 5 Total Frequency (f): 46 ? ? 25 10 5 200
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No of accident (x) 0 1 2 3 4 5 Total Frequency (f): 46 ? ? 25 10 5 200
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50. x : 10 30 50 70 90 f : 17 f1 32 f2 19 Total 120.
View SolutionFind the mean of the following frequency distribution by direct method.
 View Solution
View SolutionFind the missing frequencies in the following distribution table. It is given that the mean of these distributions is 56 and their total is 90 i.e., ∑f=90
 View Solution
View SolutionFind the mean and standard deviation of the following frequency distribution :
 View Solution
View SolutionFind the mean deviation from the median for following frequency distribution :
 View Solution
View Solution

