Find the ratio of IA:IB:IC, where l is the incentre of ΔABC.
The correct Answer is:la=rcosecA/2,lb=rcosecB/2,lc=rcosecC/2.
To find the ratio of IA:IB:IC where I is the incenter of triangle ABC, we can follow these steps:
Step 1: Understand the Incenter
The incenter I of triangle ABC is the point where the angle bisectors of the triangle intersect. It is also the center of the inscribed circle (incircle).
Step 2: Use the Angle Bisector Theorem
The lengths from the incenter to the vertices of the triangle can be expressed in terms of the angles of the triangle. Specifically, we have:
- IA=RsinA2
- IB=RsinB2
- IC=RsinC2
where R is the radius of the incircle.
Step 3: Write the Ratios
Now we can write the ratios of IA,IB, and IC:
IA:IB:IC=RsinA2:RsinB2:RsinC2
Step 4: Simplify the Ratios
Since R is common in all three terms, we can cancel it out:
IA:IB:IC=1sinA2:1sinB2:1sinC2
Step 5: Convert to Cosecant
This can be rewritten using cosecant:
IA:IB:IC=cscA2:cscB2:cscC2
Final Answer
Thus, the ratio IA:IB:IC is:
cscA2:cscB2:cscC2
---
The incenter I of triangle ABC is the point where the angle bisectors of the triangle intersect. It is also the center of the inscribed circle (incircle).
The lengths from the incenter to the vertices of the triangle can be expressed in terms of the angles of the triangle. Specifically, we have:
- IA=RsinA2
- IB=RsinB2
- IC=RsinC2
Now we can write the ratios of IA,IB, and IC:
IA:IB:IC=RsinA2:RsinB2:RsinC2
Since R is common in all three terms, we can cancel it out:
IA:IB:IC=1sinA2:1sinB2:1sinC2
This can be rewritten using cosecant:
IA:IB:IC=cscA2:cscB2:cscC2
Thus, the ratio IA:IB:IC is:
cscA2:cscB2:cscC2
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Find the ratio of the circum-radius and the inradius of ΔABC, whose sides are in the ratio 4:5:6.
View SolutionThe position vectors of the vertices A,BandC of triangle are ˆi+ˆj,ˆj+ˆkandˆi+ˆk, respectively. Find the unit vectors ˆr lying in the plane of ABC and perpendicular to IA, where I is the incentre of the triangle.
View SolutionFind the ratio of:
250 mL to 2 L.
View SolutionFind the distance between the circumcentre and the incentre of the ΔABC.
View SolutionIn a ΔABC, if (II1)2+(I2I3)2=λR2, where I denotes incentre, I1,I2andI3 denote centres of the circles escribed to the sides BC, CA and AB respectively and R be the radius of the circum circle of ΔABC. Find λ.
View SolutionA cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.
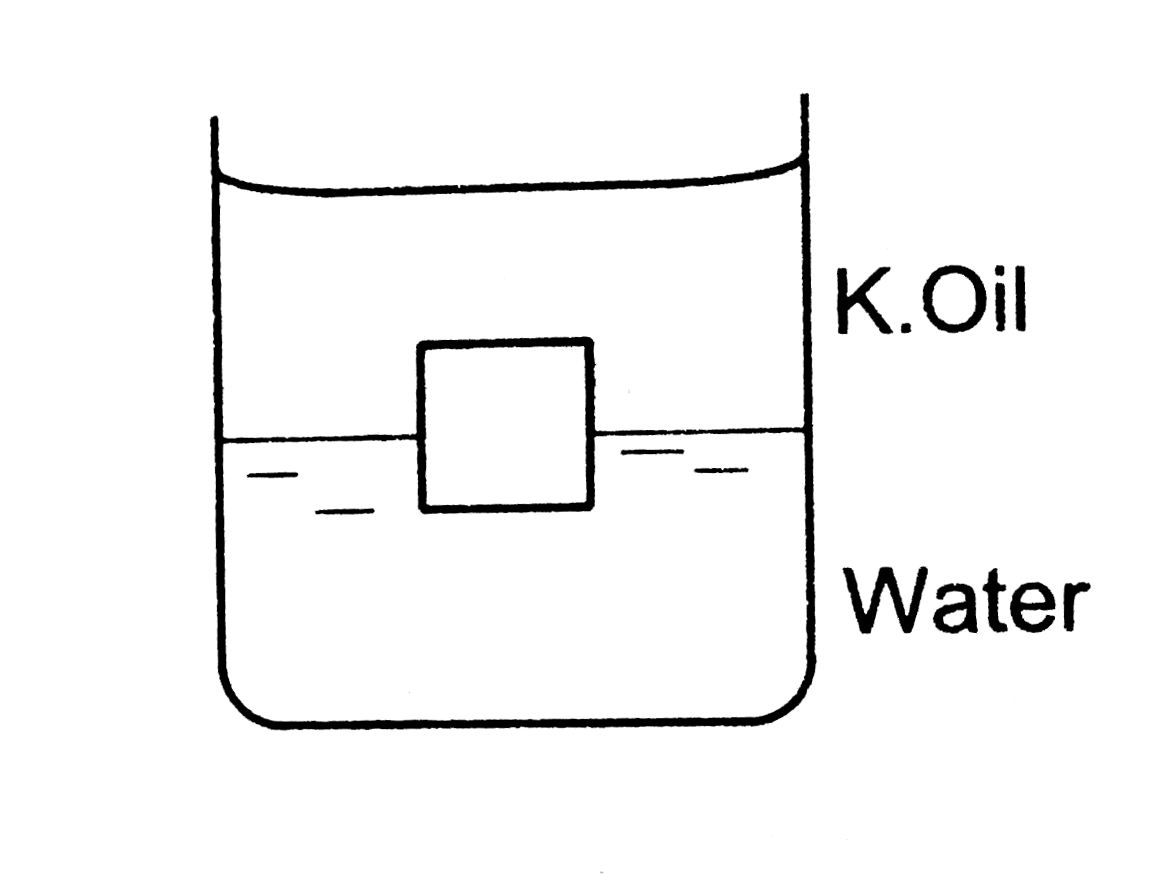
View SolutionInDeltaABC,<B=90∘,tanA=34and length of BC =180 m, ten find the length of hypotenuse of ΔABC.
View SolutionFind the length of AB for the given ΔABC.
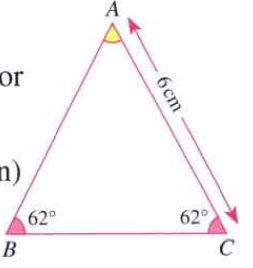
View SolutionFind the perimeter of ΔABC, if AP=12 cm

View SolutionFind the coordinats of the incentre of the triangle whose sides are x=3,y=4and4x+3y=12. Also find the centroid.
View Solution
