Find the ratio of the areas of the portion between the circle $x^{2} + y^{2} = a^{2}$ and straight line $x = \frac{a}{2}$

Video Solution

Text Solution

Verified by Experts

Let the line $x = \frac{a}{2}$ intersect the circle $x^{2} + y^{2} = a^{2}$ at points P and Q. Therefore two parts of the circle divided by the line are PAQP and PBQP.

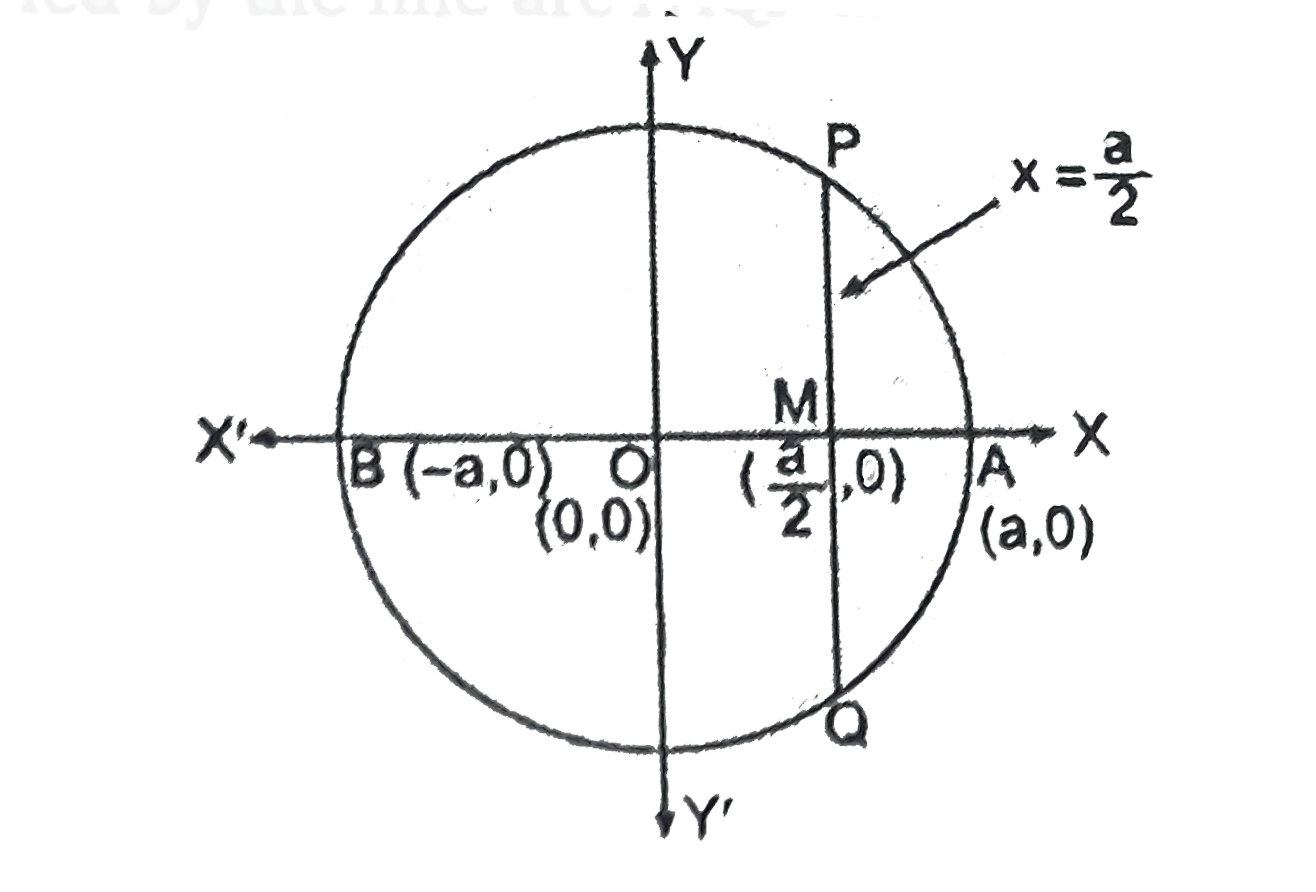
Now area of PAQP
$= 2 \times$ area of PAMP
$= 2 \times \int_{a / 2}^{a} \sqrt{a^{2} - x^{2}} d x$
$= 2 {[\frac{x}{2} \sqrt{a^{2} - x^{2}} + \frac{a^{2}}{2} {sin}^{- 1} \frac{x}{a}]}_{a / 2}^{- 1}$
$= 2 [(0 + \frac{a^{2}}{2} {sin}^{- 1} 1) - (\frac{a}{4} . \frac{a \sqrt{3}}{2} + \frac{a^{2}}{2} {sin}^{- 1} \frac{1}{2})]$
$= 2 (\frac{a^{2} π}{4} - \frac{a^{2} \sqrt{3}}{8} - \frac{a^{2} π}{12})$
$= \frac{6 a^{2} π - 3 a^{2} \sqrt{3} - 2 a^{2} π}{12}$
$= \frac{a^{2} (4 π - 3 \sqrt{3})}{12} s q .$ units.
and area of PBQP = Area of circle - Area of PAQP
$= π a^{2} - \frac{a^{2} (4 π - 3 \sqrt{3})}{12}$
$= \frac{12 π a^{2} - 4 π a^{2} + 3 \sqrt{3} a^{2}}{12} = \frac{a^{2} (8 π + 3 \sqrt{3})}{12}$
$∴$ Area of PBQP : Area of PAQP
$= \frac{a^{2} (8 π + 3 \sqrt{3})}{12} : \frac{a^{2} (4 π - 3 \sqrt{3})}{12}$
$= (8 π + 3 \sqrt{3}) : (4 π - 3 \sqrt{3})$ .

What is the area of the region enclosed between the curve $y^{2} = 2 x$ and the straight line y=x?
A2/3 sq unit
B4/3sq unit
C1/3 sq unit
D1 sq. unit
The area of smaller part between the circle $x^{2} + y^{2} = 4$ and the line x=1 is
A $\frac{4 π}{3} - \sqrt{3}$
B $\frac{8 π}{3} - \sqrt{3}$
C $\frac{4 π}{3} + \sqrt{3}$
D $\frac{5 π}{3} + \sqrt{3}$