Find the value of p , if the mean of the following distribution is 20. x:15,17,19,20+p,23 and f : 2, 3, 4, 5p, 6
To find the value of p given that the mean of the distribution is 20, we will follow these steps:
Step 1: Set up the data
We have the values of x and f as follows:
- x:15,17,19,20+p,23
- f:2,3,4,5p,6
Step 2: Create a table for f×x
Now, we will calculate fi×xi for each pair:
- For x=15, f=2:
f×x=2×15=30
- For x=17, f=3:
f×x=3×17=51
- For x=19, f=4:
f×x=4×19=76
- For x=20+p, f=5p:
f×x=5p×(20+p)=100p+5p2
- For x=23, f=6:
f×x=6×23=138
Step 3: Sum the values of f×x and f
Now we will sum these values:
1. Sum of fi×xi:
∑fi×xi=30+51+76+(100p+5p2)+138=295+100p+5p2
2. Sum of fi:
∑fi=2+3+4+5p+6=15+5p
Step 4: Use the formula for the mean
The mean ¯x is given by:
¯x=∑fi×xi∑fi
Given that the mean is 20, we can set up the equation:
20=295+100p+5p215+5p
Step 5: Cross-multiply to eliminate the fraction
Cross-multiplying gives:
20(15+5p)=295+100p+5p2
Expanding this:
300+100p=295+100p+5p2
Step 6: Simplify the equation
Subtract 100p from both sides:
300=295+5p2
Subtract 295 from both sides:
5=5p2
Step 7: Solve for p2
Dividing both sides by 5:
1=p2
Step 8: Find the value of p
Taking the square root of both sides:
p=±1
Since p represents a frequency, it cannot be negative. Therefore:
p=1
Final Answer
The value of p is 1.
---
We have the values of x and f as follows:
- f:2,3,4,5p,6
Now, we will calculate fi×xi for each pair:
f×x=2×15=30
- For x=17, f=3:
f×x=3×17=51
- For x=19, f=4:
f×x=4×19=76
- For x=20+p, f=5p:
f×x=5p×(20+p)=100p+5p2
- For x=23, f=6:
f×x=6×23=138
Now we will sum these values:
∑fi×xi=30+51+76+(100p+5p2)+138=295+100p+5p2
∑fi=2+3+4+5p+6=15+5p
The mean ¯x is given by:
¯x=∑fi×xi∑fi
Given that the mean is 20, we can set up the equation:
20=295+100p+5p215+5p
Cross-multiplying gives:
20(15+5p)=295+100p+5p2
Expanding this:
300+100p=295+100p+5p2
Subtract 100p from both sides:
300=295+5p2
Subtract 295 from both sides:
5=5p2
Dividing both sides by 5:
1=p2
Taking the square root of both sides:
p=±1
Since p represents a frequency, it cannot be negative. Therefore:
p=1
The value of p is 1.
Topper's Solved these Questions
Similar Questions
Find the value of p, if the mean of the following distribution is 18 :
 View Solution
View SolutionFind the value of P if the mean of the following distribution is 7.5
 View Solution
View SolutionFind the value of p, if the mean of following distribution is 20.
 View Solution
View SolutionFind the value of p, if mean of the following distribution is 7.5.
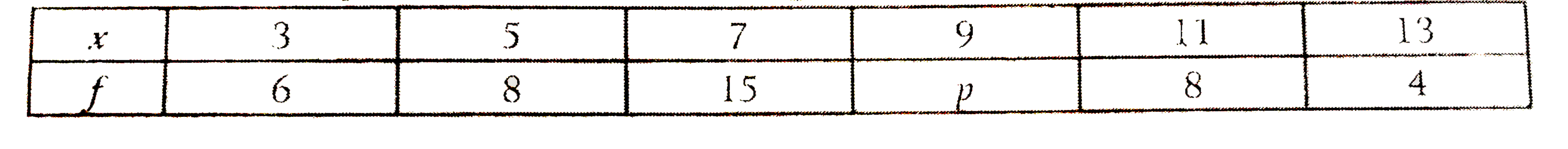 View Solution
View SolutionFind the value of p, if the mean of the following distribution is 20 15 17 19 23 2 3 4 5 6
View SolutionFind the value of p, if the mean of the following distribution is 7.5. x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the value of p if the mean of the following distribution is 7.5. 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionFind the value of p , the mean of the following distribution is 7.5 x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
View SolutionIf the mean of the following distribution is 6, find the value of p
View SolutionIf the mean of the following distribution is 3 find the value of p.
 View Solution
View Solution

