Find the values of α such that the variable point (α,tanα) lies inside the triangle whose sides are
y=x+√3−π3,x+y+1√3+π6=0 and x−π2=0
The correct Answer is:−π6<α<π3
Given lines are
y=x+√3−π3 (1)
x+y+1√3+π6=0 (2)
and x−π2=0 (3)
Variable point (α,tanα) lies on the curve y=tan x.
So, we draw the given lines and curve y=tan x.
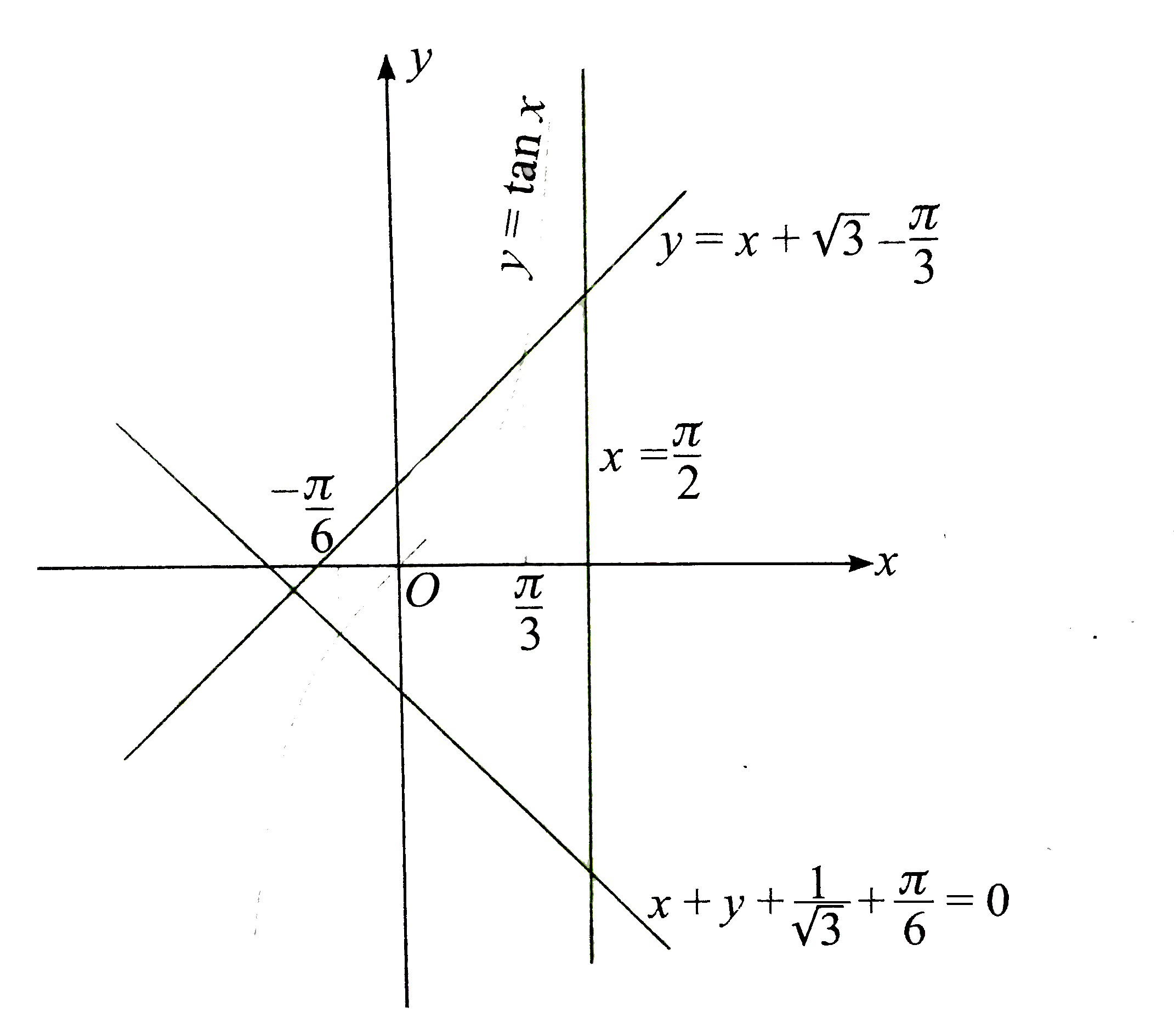
By hit and trial method, we find that line (1) cuts the curve.
y=tanxforx=π3 and line (2) cuts the curve for x=−π6.
Hence, point (α,tanα) lies inside the triangle if−π6<α<π6.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.58videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.65videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.37videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The range of values of α in the interval (0,π) such that the points (3,5) and (sinα,cosα) lie on the same side of the line x+y−1=0 is
A(0,π/4)B(π/4,π/2)C(0,π/2)DNone
Find the value of alpha for which the P(2+cosα,sinα) lies inside the triangle having vertices (2,0),(−7,0)and(−1,√3).
View SolutionDetermine all the values of α for which the point (α,α2) lies inside the triangle formed by the lines. 2x+3y−1=0 x+2y−3=0 5x−6y−1=0
View SolutionThe range of value of α such that (0,α) lies on or inside the triangle formed by the lines y + 3x + 2 = 0, 3y - 2x - 5 = 0, 4y + x - 14 =0 is
View SolutionIf point P(α,α2−2) lies inside the triangle formed by the lines x+y=1,y=x+1andy=−1 then α∈
View SolutionFind the values of α lying between 0 and π for which the inequality : tanα>tan3α is valid.
View SolutionStatement 1: The value of α for which the point (α,α2) lies inside the triangle formed by the lines x=0,x+y=2 and 3y=x is (0,1). Statement 2: The parabola y=x2 meets the linex+y=2 at(0,1).
View SolutionIf the point (α,α4) lies on or inside the triangle formed by lines x2y+xy2−2xy=0, then the largest value of α is .
View Solution

