Following is the distribution of I.Q. of 100 students. Find the median I.Q. I.Q.55-64 65-74 75-84 85-94 95-104 105-114 115-124 125-134 135-144 No. of Students: 1 2 9 22 33 22 8 2 1
To find the median of the given distribution of IQ scores, we will follow these steps:
Step 1: Prepare the Class Intervals
We need to convert the exclusive class intervals into inclusive class intervals. The given class intervals are:
- 55-64
- 65-74
- 75-84
- 85-94
- 95-104
- 105-114
- 115-124
- 125-134
- 135-144
The inclusive class intervals will be:
- 54.5 to 64.5
- 64.5 to 74.5
- 74.5 to 84.5
- 84.5 to 94.5
- 94.5 to 104.5
- 104.5 to 114.5
- 114.5 to 124.5
- 124.5 to 134.5
- 134.5 to 144.5
Step 2: Create a Frequency Table
Next, we will create a frequency table with the cumulative frequency.
| Class Interval | Frequency | Cumulative Frequency |
|----------------|-----------|----------------------|
| 54.5 - 64.5 | 1 | 1 |
| 64.5 - 74.5 | 2 | 3 |
| 74.5 - 84.5 | 9 | 12 |
| 84.5 - 94.5 | 22 | 34 |
| 94.5 - 104.5 | 33 | 67 |
| 104.5 - 114.5 | 22 | 89 |
| 114.5 - 124.5 | 8 | 97 |
| 124.5 - 134.5 | 2 | 99 |
| 134.5 - 144.5 | 1 | 100 |
Step 3: Calculate N and N/2
The total number of students (N) is 100. Therefore, N/2 = 100/2 = 50.
Step 4: Identify the Median Class
We need to find the cumulative frequency just greater than N/2 (which is 50). From the cumulative frequency column, we see that the cumulative frequency of 67 (which corresponds to the class interval 94.5 - 104.5) is the first cumulative frequency greater than 50. Thus, the median class is 94.5 - 104.5.
Step 5: Apply the Median Formula
Now we will use the median formula:
Median=L+(N/2−Ff)×h
Where:
- L = lower limit of the median class = 94.5
- F = cumulative frequency of the class before the median class = 34
- f = frequency of the median class = 33
- h = width of the median class = upper limit - lower limit = 104.5 - 94.5 = 10
Substituting the values into the formula:
Median=94.5+(50−3433)×10
=94.5+(1633)×10
=94.5+4.85≈99.35
Final Answer
The median IQ of the students is approximately 99.35.
We need to convert the exclusive class intervals into inclusive class intervals. The given class intervals are:
- 55-64
- 65-74
- 75-84
- 85-94
- 95-104
- 105-114
- 115-124
- 125-134
- 135-144
- 54.5 to 64.5
- 64.5 to 74.5
- 74.5 to 84.5
- 84.5 to 94.5
- 94.5 to 104.5
- 104.5 to 114.5
- 114.5 to 124.5
- 124.5 to 134.5
- 134.5 to 144.5
Next, we will create a frequency table with the cumulative frequency.
|----------------|-----------|----------------------|
| 54.5 - 64.5 | 1 | 1 |
| 64.5 - 74.5 | 2 | 3 |
| 74.5 - 84.5 | 9 | 12 |
| 84.5 - 94.5 | 22 | 34 |
| 94.5 - 104.5 | 33 | 67 |
| 104.5 - 114.5 | 22 | 89 |
| 114.5 - 124.5 | 8 | 97 |
| 124.5 - 134.5 | 2 | 99 |
| 134.5 - 144.5 | 1 | 100 |
The total number of students (N) is 100. Therefore, N/2 = 100/2 = 50.
We need to find the cumulative frequency just greater than N/2 (which is 50). From the cumulative frequency column, we see that the cumulative frequency of 67 (which corresponds to the class interval 94.5 - 104.5) is the first cumulative frequency greater than 50. Thus, the median class is 94.5 - 104.5.
Now we will use the median formula:
Median=L+(N/2−Ff)×h
Where:
- L = lower limit of the median class = 94.5
- F = cumulative frequency of the class before the median class = 34
- f = frequency of the median class = 33
- h = width of the median class = upper limit - lower limit = 104.5 - 94.5 = 10
Median=94.5+(50−3433)×10
=94.5+(1633)×10
=94.5+4.85≈99.35
The median IQ of the students is approximately 99.35.
Topper's Solved these Questions
Similar Questions
Find the image of the following sets under the mapping f(x)=x4−8x3+22x2−24x+10 (i) (−∞,1)
View SolutionFollowing frequency distribution given the weights of 38 students of a class: Weight in Kg: 31-35 36-40, 41-45, 46-50, 51-55, 56-60 61-65, 66-70 71-75 No. of students 9 5 14 3 1 2 2 1 1 Find the probability that weight of a student in the class is: (i)at most 60 kg (ii)at least 36 kg (iii)not more than 50kg. Also define two events in this context, one having probability 0 and the other having probability 1.
View Solution
Knowledge Check
- Question 1 - Select One
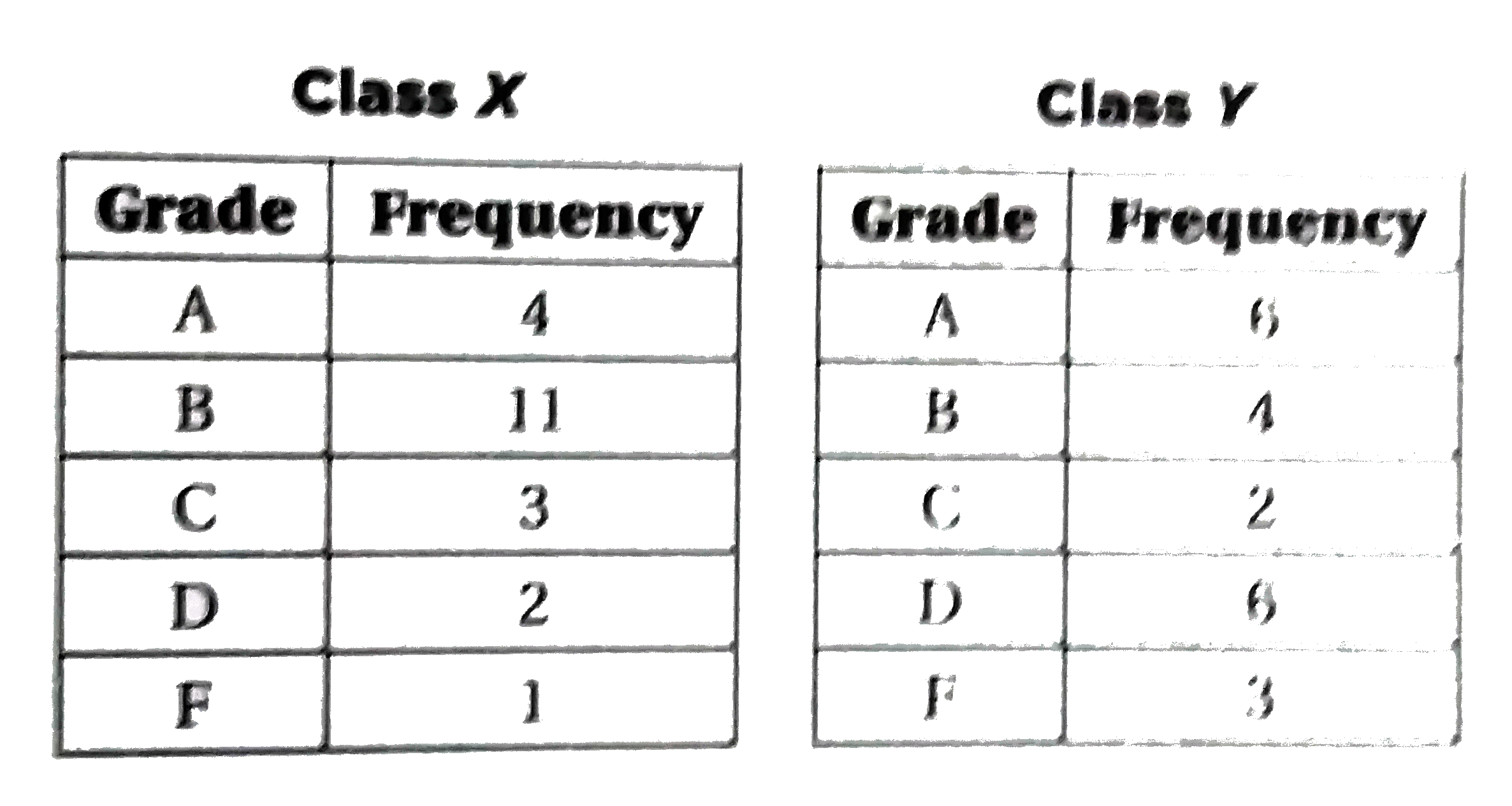
The tables give the distribution of grades for 21 students in two different college mathematics classes. For purposes of making statistical calculations, A=4,B=3,C=2,D=1,andF=0. Which of the following statements is true about the data shown for these two classes?
I. The standard deviation of grades is greater for class X.
II. the standard deviation of grades is greater for class Y.
III. The median letter grade is the same for classes X and Y.AI onlyBII onlyCI and III onlyDII and III only
If the x-coordinate of a point P on the join of Q(22,1)andR(5,1,−2)is4, then find its z− coordinate.
View SolutionWrite the following sets m the setbuilder form:(i) (3,6,9,12} (ii) {2,4,8,16,32} (iii) {5,25,125,625}(iv) {2,4,6,...} (v) {1,4,9,...,100}
View SolutionFind the distance between the following pairs of points :
(i) (-2, 1, -3) and (4, 3, -6)
(ii) (9, -12, -8) and (0,0,0)
(iii) (2,1,-3) and (2, 3, -3)
(iv) (1,0,0) and (4, 4, 5)View SolutionAn insurance company selected 2000 drivers at random in a particular city to find a relationship between age and accidents. The obtained are given in the following table: Age of Drivers (in years) Accidents in one year 0 1 2 3 over 3 18-29 30-50 above 50 440 505 360 160 125 45 110 60 35 61 22 15 35 18 9 Find the probability of the following events for a driver chosen at random from the life city: i) being 18-29 years of age and having exactly 3 accidents in one year. ii) being 30-50 years of age and having one or more accidents in a year. iii) having no accidents in one year.
View SolutionConstruct a frequency distribution table for the following data, taking class-intervals 4−6,6−8, ............., 14−16.
11.5,6.3,7.8,9.2,10.5,
4.5,6,8.3,12.5,15.8,
7.4,5.3,8.4,15.2,8.9,
9.8,8.25,6.5,5.8,10.5,
14.2,15.3,11.7,9.9,8.8,
6.6,4.3,4.7,9.4,10.1,
15.5,14.4,12.2,7.7,5.5.View SolutionThe median for the following frequency distribution is :
xi :123456789fi :810111620251596View SolutionFind the median for the following frequency distribution :
Marks obtained(xi)293234274237Number of students(fi)25101284View Solution

