Following is the graph of y = f'(x) and f(0) = 0 .

(a) What type of function y = f'(x) is ? Odd or even?
(b) What type of function y = f(x) is ? Odd or even?
(c) What is the value of ∫a−af(x)dx?
(d) Has y = f(x) point of inflection?
(e) What is the nature of y = f(x)? Monotonic or non-monotonic?Solution in Bengali
(a) The graph of y = f'(x) is symmetrical about the y-axis, so f(x) is an even function.
(b) f(0) = 0, so f(x) is an odd function [derivative of an odd function is even].
(c) As f(x) is odd, so a∫−af(x)dx=0
(d) f''(x)>0asx<0andf''(x)<0as x>0. Therefore, x = 0 is the point of inflexion.
(e) f'(x)≤0,∀x, so f(x) is always decreasing.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.17
1 Videos
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
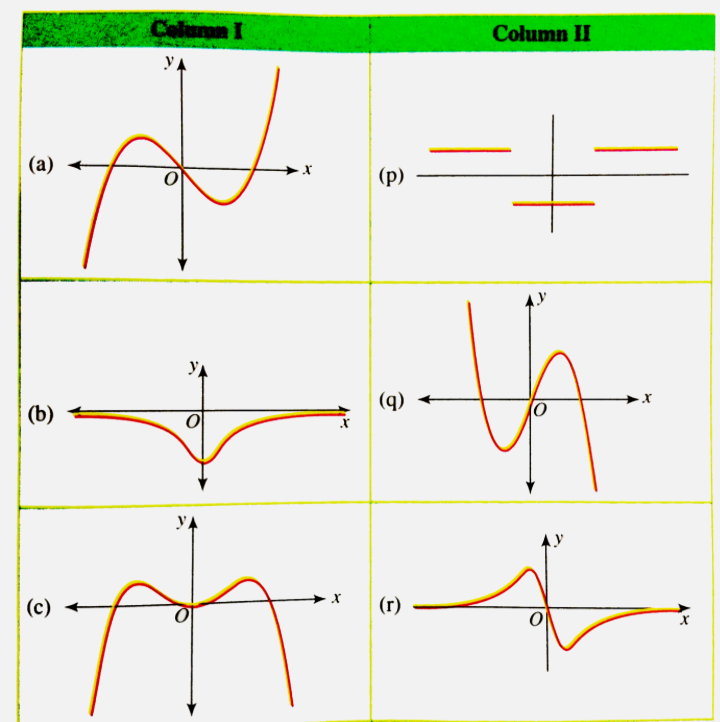
Match the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.

View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionIf the function / satisfies the relation f(x+y)+f(x−y)=2f(x),f(y)∀x,y∈Randf(0)≠0 , then f(x)isa≠venfunction f(x)isanoddfunction Iff(2)=a,thenf(−2)=a Iff(4)=b,thenf(−4)=−b
View SolutionLet f(x) be real valued and differentiable function on R such that f(x+y)=f(x)+f(y)1−f(x).f(y) f(x) is Odd function Even function Odd and even function simultaneously Neither even nor odd
View SolutionFollowing is the graph of y = f'(x) and f(0) = 0 .

(a) What type of function y = f'(x) is ? Odd or even?
(b) What type of function y = f(x) is ? Odd or even?
(c) What is the value of ∫a−af(x)dx?
(d) Has y = f(x) point of inflection?
(e) What is the nature of y = f(x)? Monotonic or non-monotonic?
View Solution∫a−af(x)dx=2∫a0f(x)dx, if f is an even function
0, if f is an odd function.
View SolutionThe order of reactivity of halogens is
(A) F>Cl>Br>I
(B) F < Cl < Br < I
(C) F < Cl > Br < I
(D) F < Cl < Br> I
View Solution[" Let "f(x+y)=f(x)+f(y)" for all "],[x,y in R" .Then "],[" (A) "f(x)" is an even function "],[" (B) "f(x)" is an odd function "],[" (C) "f(0)=0],[" (D) "f(n)=nf(1),n in N]
View SolutionLet f(x) be real valued and differentiable function on R such that f(x+y)=f(x)+f(y)1−f(x).f(y) f(x) is Odd function Even function Odd and even function simultaneously Neither even nor odd
View SolutionFollowing is the graph of y = f'(x) and f(0) = 0 .

(a) What type of function y = f'(x) is ? Odd or even?
(b) What type of function y = f(x) is ? Odd or even?
(c) What is the value of ∫a−af(x)dx?
(d) Has y = f(x) point of inflection?
(e) What is the nature of y = f(x)? Monotonic or non-monotonic?
View SolutionFill in the blanks: br The function f(x)=e2x is increasing on R…….
View SolutionStatement True/ False: br If f(x)>0 then the function f(x) is said to be decreasing.
View SolutionProve that ∫a−a f(x) dx = 0, if f(x) is odd function,
=2∫a0 f(x) dx, if f(x) is an even function
View SolutionIf f(x+y)+f(x-y)=2f(x).f(y)∀x,y∈R. f(0)≠0, find if f(x) is even or odd function.
View SolutionIf y=f(x)isanevenfunctionsuchtˆf^(')(0)∃,thenf^(')(0) =
View Solution
