Following is the graph of y = f'(x) and f(0) = 0 .

(a) What type of function y = f'(x) is ? Odd or even?
(b) What type of function y = f(x) is ? Odd or even?
(c) What is the value of ∫a−af(x)dx?
(d) Has y = f(x) point of inflection?
(e) What is the nature of y = f(x)? Monotonic or non-monotonic?
(a) The graph of y = f'(x) is symmetrical about the y-axis, so f(x) is an even function.
(b) f(0) = 0, so f(x) is an odd function [derivative of an odd function is even].
(c) As f(x) is odd, so a∫−af(x)dx=0
(d) f''(x)>0asx<0andf''(x)<0as x>0. Therefore, x = 0 is the point of inflexion.
(e) f'(x)≤0,∀x, so f(x) is always decreasing.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- FUNCTIONSBOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Question Bank
30 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
Similar Questions
Knowledge Check
If f(x) is an even function, then what is ∫π0f(cosx) dx equal to ?
A0B∫π/20f(cosx)dxC2∫π20f(cosx)dxD1If f(x) is a linear function and the slope of y=f(x) is 12, what is the slope of y=f−1(x) ?
A−2B−12C12D2Let a function is defined as f(x)=ax+a−x2,a>0, what is the value of f(x+y)+f(x−y)?
Af(x)+f(y)Bf(x)f(y)C2f(x)f(y)Df(x)f(y)
Following is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
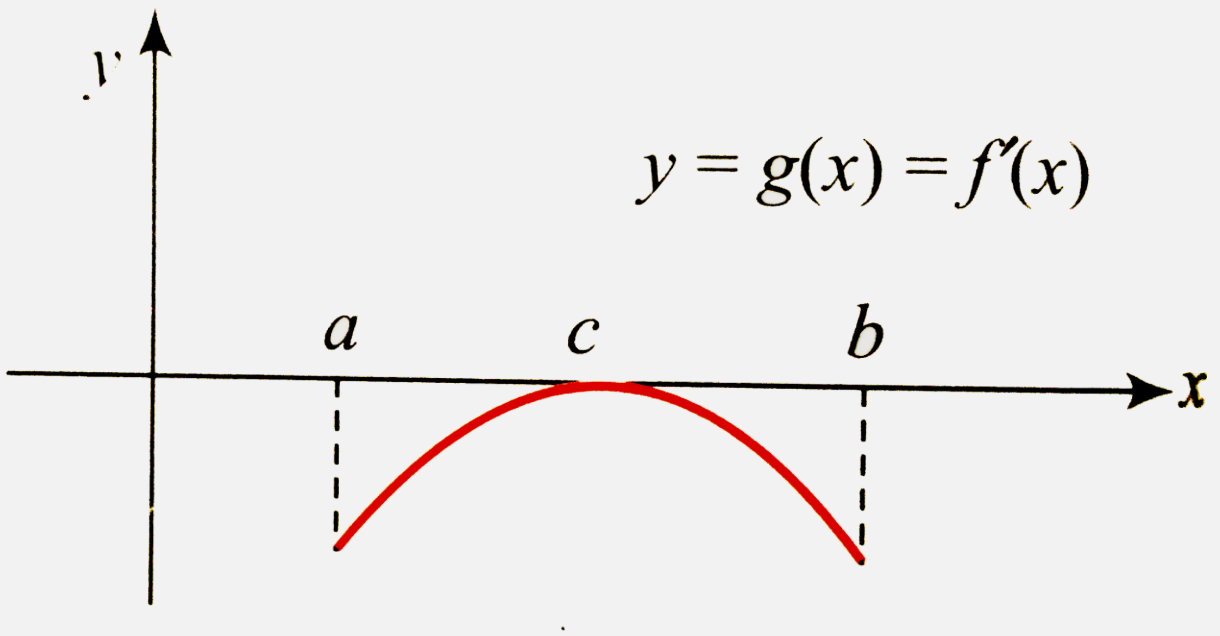
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?

View SolutionThe graph of y=f''(x) for a function f is shown.
Number of points of inflection for y=f(x) is….. .

View SolutionIf f(x) is an odd function, then the curve y=f(x) is symmetric
View SolutionIf f(x) is an odd function, then the curve y=f(x) is symmetric
View Solution
