For every pair (x, y) in the rectangular coordinate plane, f:(x,y)→(x,−8x+3y). What is the set of points for which f:(x,y)→(x,y) ?
The point (-4, 0)
The point (4, 12)
The set of points (x, y) that satisfy the equation x = 4y
The set of points (x, y) that satisfy the equation y = 4x
The correct Answer is:D
To solve the problem, we need to find the set of points (x,y) such that the function f defined by f(x,y)=(x,−8x+3y) is equal to (x,y). This means we need to solve the equation:
f(x,y)=(x,y)
This translates to:
(x,−8x+3y)=(x,y)
From this, we can equate the corresponding components:
1. The x-coordinates:
x=x
This equation is always true and does not provide any new information.
2. The y-coordinates:
−8x+3y=y
Now, we will solve the second equation for y:
Step 1: Rearranging the equation
Subtract y from both sides:
−8x+3y−y=0
This simplifies to:
−8x+2y=0
Step 2: Isolating y
Now, we can isolate y by adding 8x to both sides:
2y=8x
Step 3: Dividing by 2
To solve for y, divide both sides by 2:
y=4x
Conclusion
The set of points (x,y) that satisfy the condition f(x,y)=(x,y) is given by the equation:
y=4x
This represents a line in the rectangular coordinate plane.
x=x
This equation is always true and does not provide any new information.
−8x+3y=y
Subtract y from both sides:
−8x+3y−y=0
This simplifies to:
−8x+2y=0
Now, we can isolate y by adding 8x to both sides:
2y=8x
To solve for y, divide both sides by 2:
y=4x
The set of points (x,y) that satisfy the condition f(x,y)=(x,y) is given by the equation:
y=4x
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the standard (x,y) coordinate plane, what is the slope of the line 3x+8y=5?
A−3B−38C35D3The function f and g are defined as f(x,y)=2x+yandg(x,y)=x+2y. What is the value of f(3,4) ?
Af(4,3)Bf(3,7)Cf(7,4)Dg(4,3)Consider the functions f(x)=√x and g(x)x2−b. In the standard (x, y) coordinate plane, y=f(g(x)) passes through the point (3, 5). What is the value of b ?
A16B4C−2D−16
The curve y=0.005x2−2x+200 for 0≤x≤200 and the line segment from F(0,200) to G(200,0) are shown in the standard (x,y) coordinate plane below.
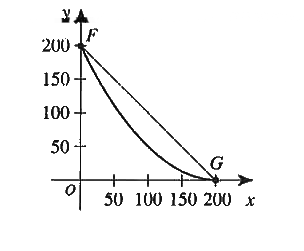
What is the y-coordinate for the point on the curve with x-coordinate 20?
View SolutionFor f(x,y)=7x+9y, what is the value of f(x,y) when y=(5x)2andx=3?
View SolutionIn the standard (x, y) coordinate plane, what are the coordinates of the center of the circle whose equation is
x2−8x+y2+10y+15=0?
View SolutionThe graph of y=f(x) is shown in the standard (x,y) coordinate plane below with points V,W,X,Y,and Z labeled .
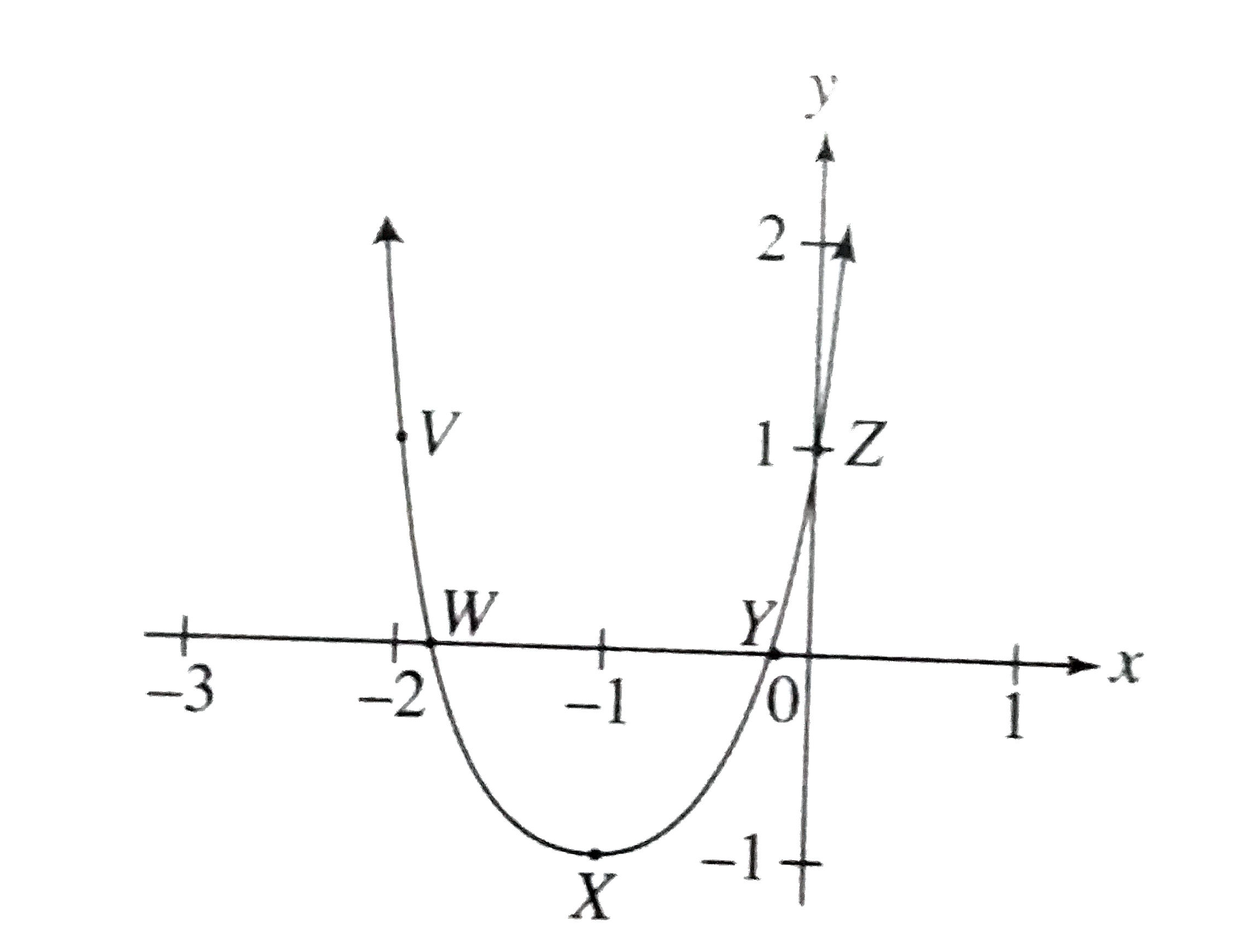
The y- intercept of the graph of y=f(x) is located at which of the following points ?
View SolutionIf 8x−2y=10and3y−9x=12, then what is the value of y−x ?
View Solution