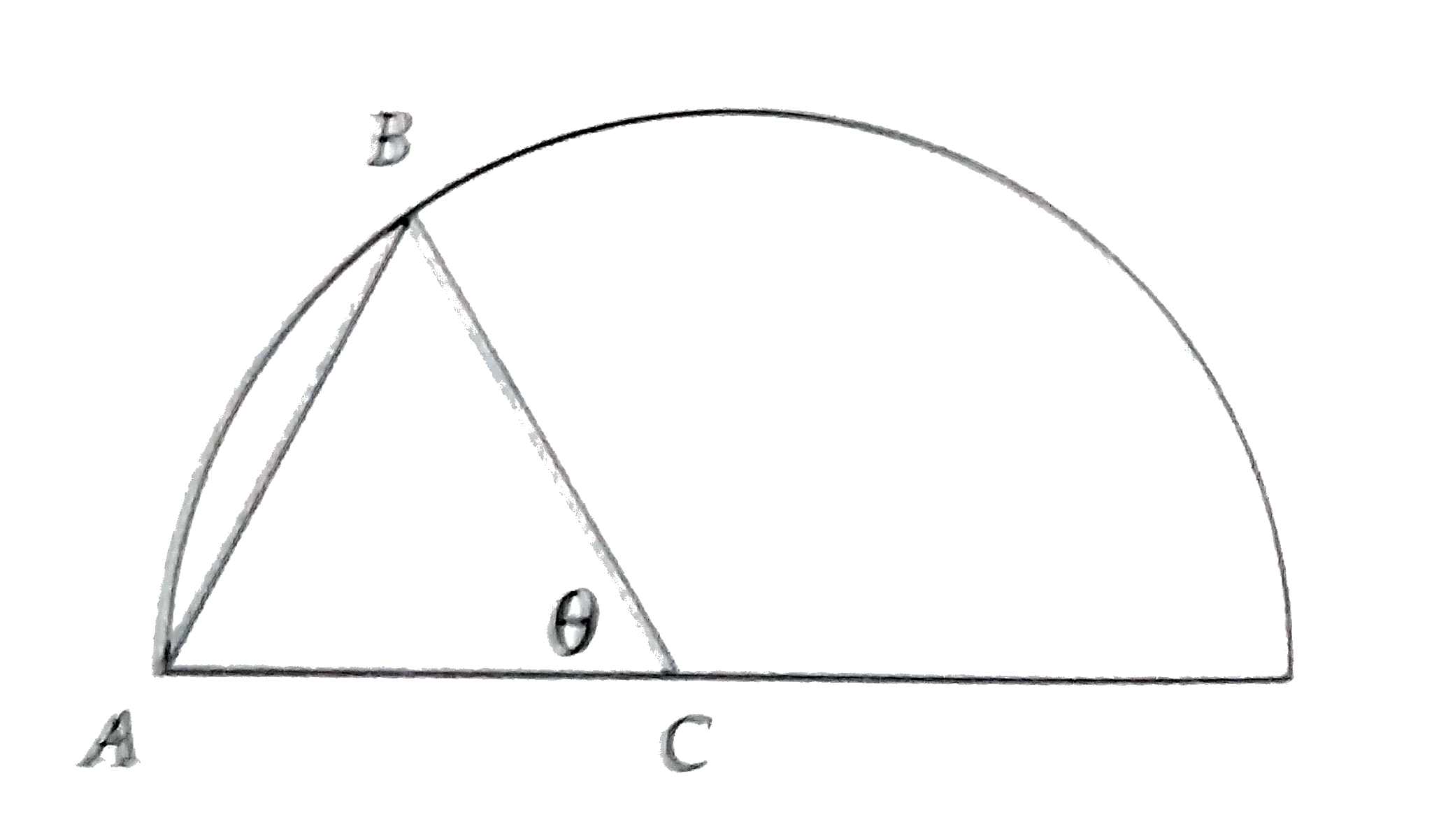
In Figure, C is the center of the semicircle, and the area of the semicircle is 8π. What is the area of triangle ABC in terms of θ ?
A
2sinθtanθ
B
4sinθ
C
8cosθ
D
8sinθ
Video Solution
Text Solution
The correct Answer is:D
The area of any triangle is 12×b×h. Call the base of triangle ABC side AC and say that the height drawn from point B to base AC meets base AC at point D.
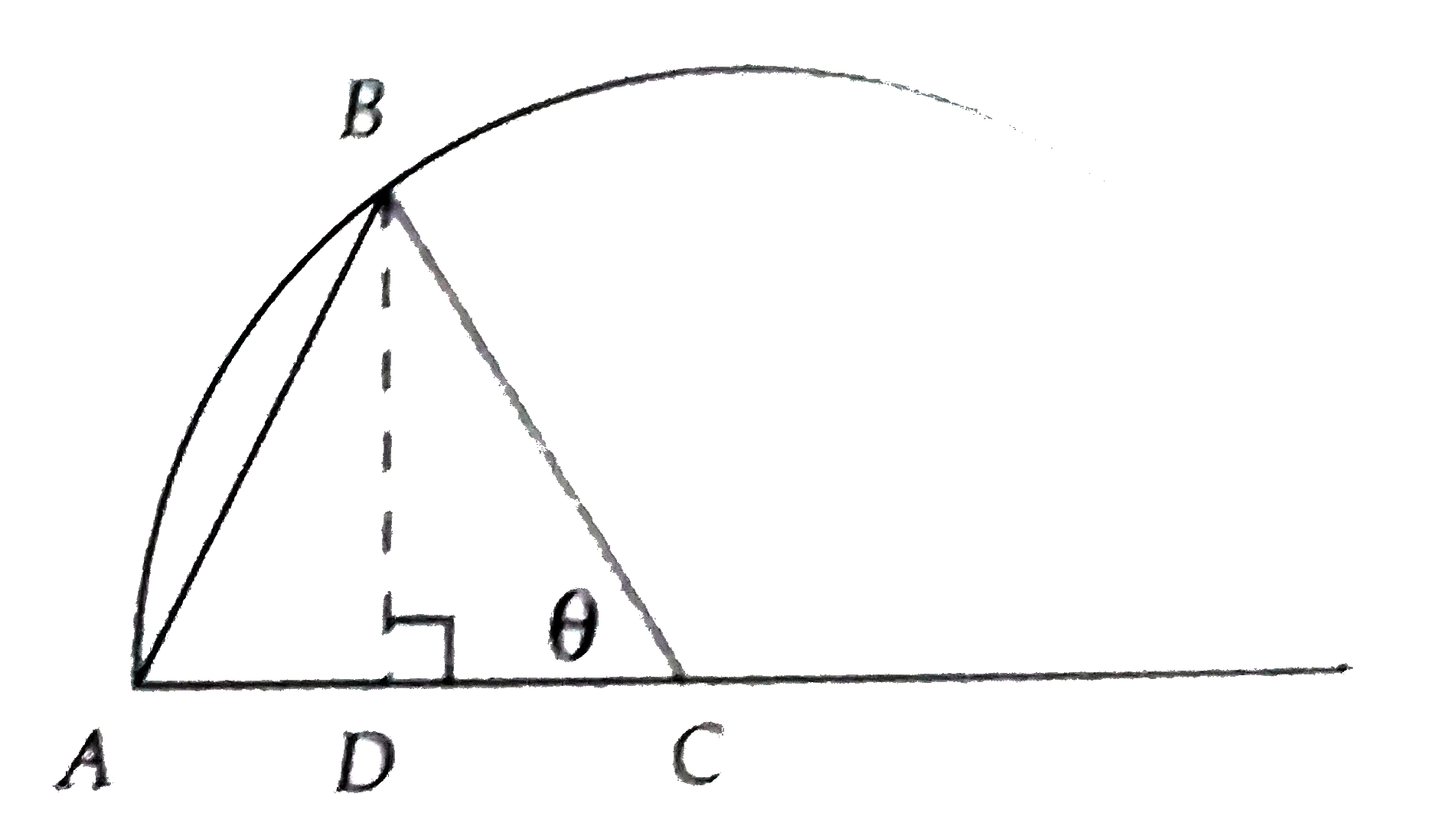
Base AC of triangle ABC is a radius of the circle. The area of the semicircle is 8π. So if the radius of the semicircile is r (in particular, r = AC = BC), then
12πr2=8π,πr2=16π,r2=16, and r = 4. So AC = 4 and BC = 4.
You can find the height BD of the triangle in terms of θ by saying that BDBC=sinθ, so BD=BCsinθ=4sinθ. Thus the base AC is 4, and the height BD is 2 sin θ. The area of the triangle is 12×AC×BD=12×4×(4sinθ)=8sinθ.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
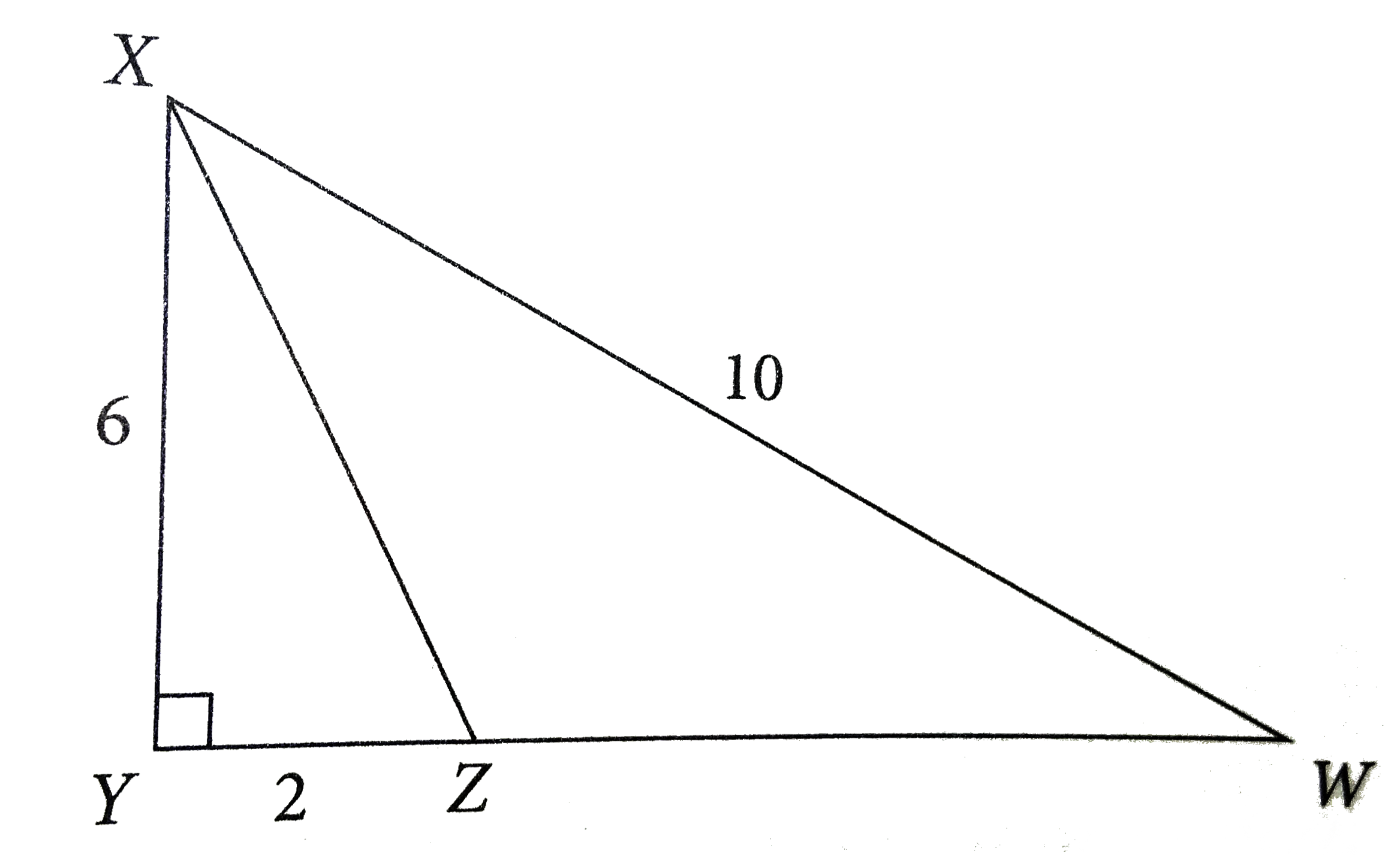
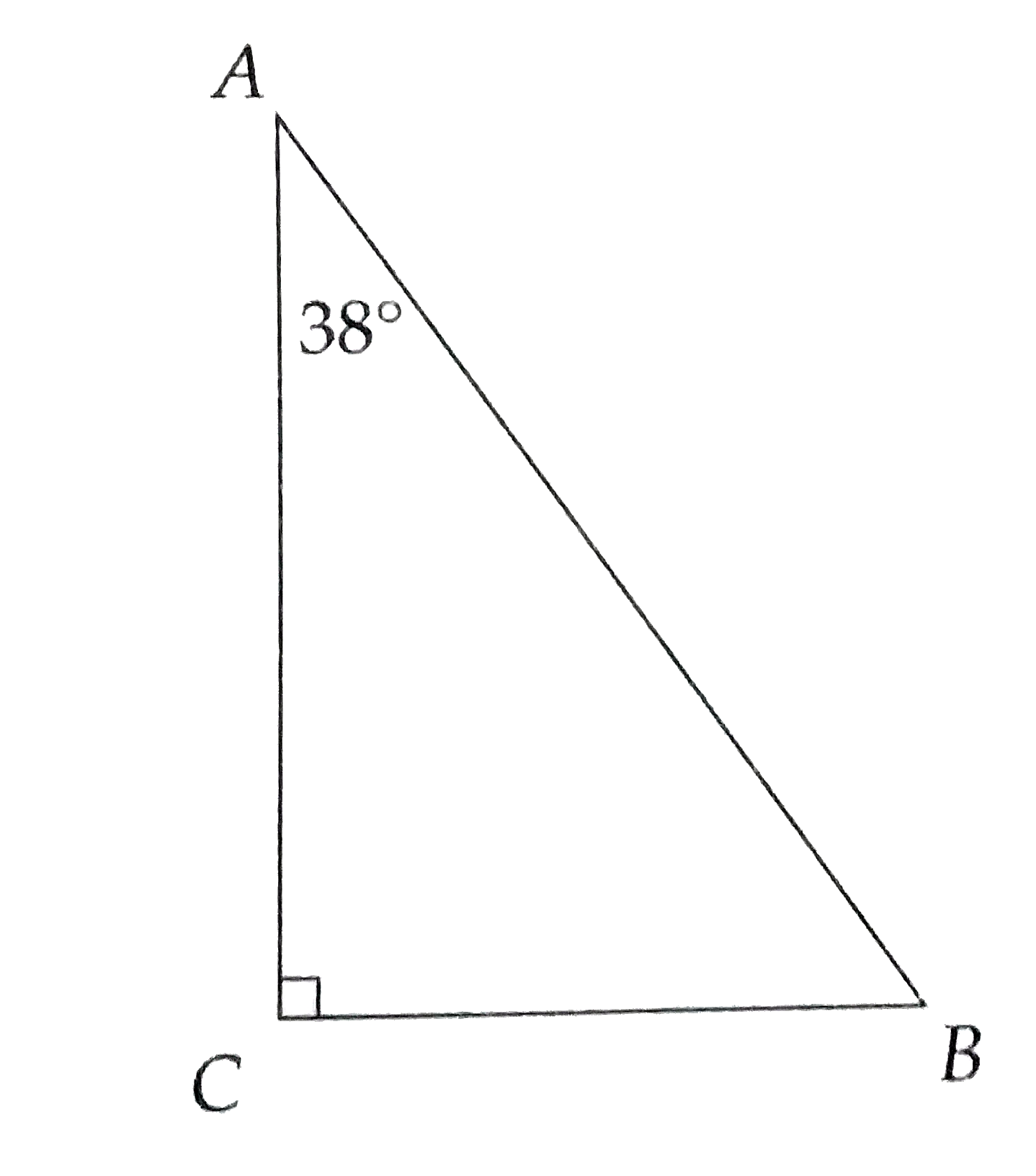
What is the area of triangle WXZ in the figure above?A6B12C18D24 - Question 2 - Select One
In the figure, what is the area of ΔABC?
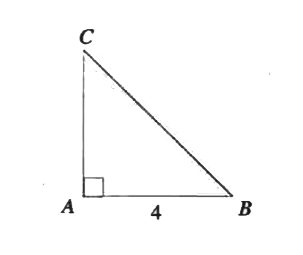 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information given - Question 3 - Select One
In the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2
In a ΔABC, a semicircle is inscribed, whose diameter lies on the side c. Then the radius of the semicircle is (Where Δ is the area of the triangle ABC)
View SolutionIf the area of triangle ABC is 15, what is the length of AC ?
 View Solution
View Solution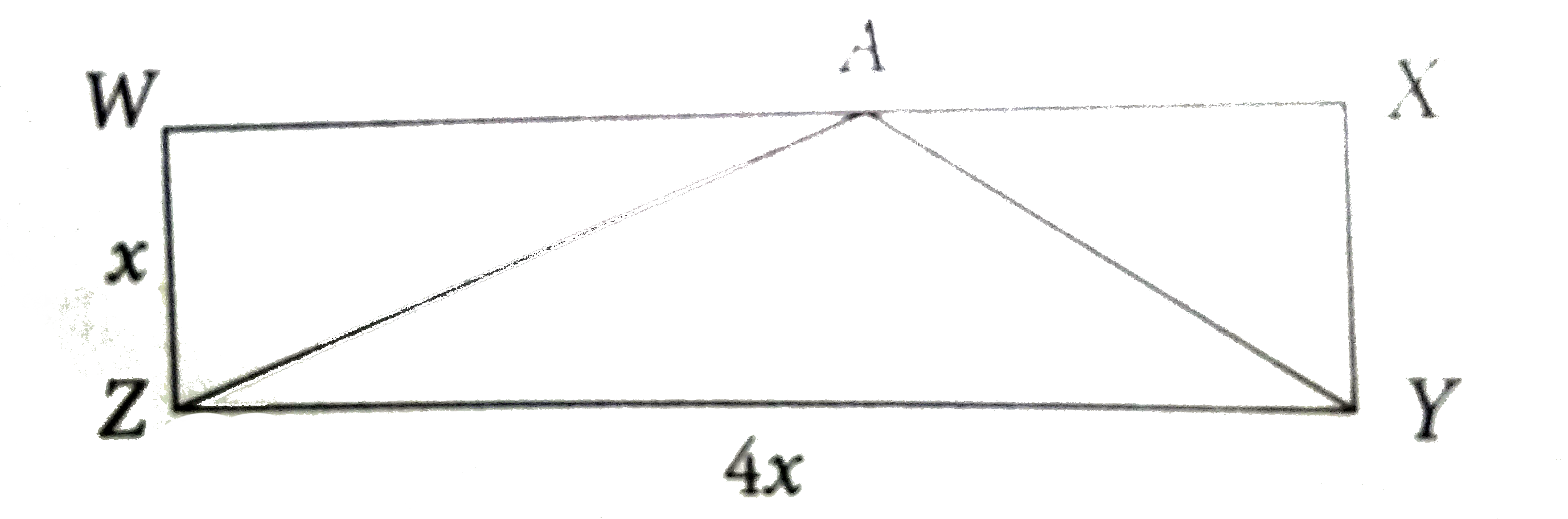
In the figure above, what is the area of triangle YAZ?View SolutionIn the figure, ABCD is a rectangle, and the area of ΔACE is 10. What is the area of the rectangle?
 View Solution
View Solution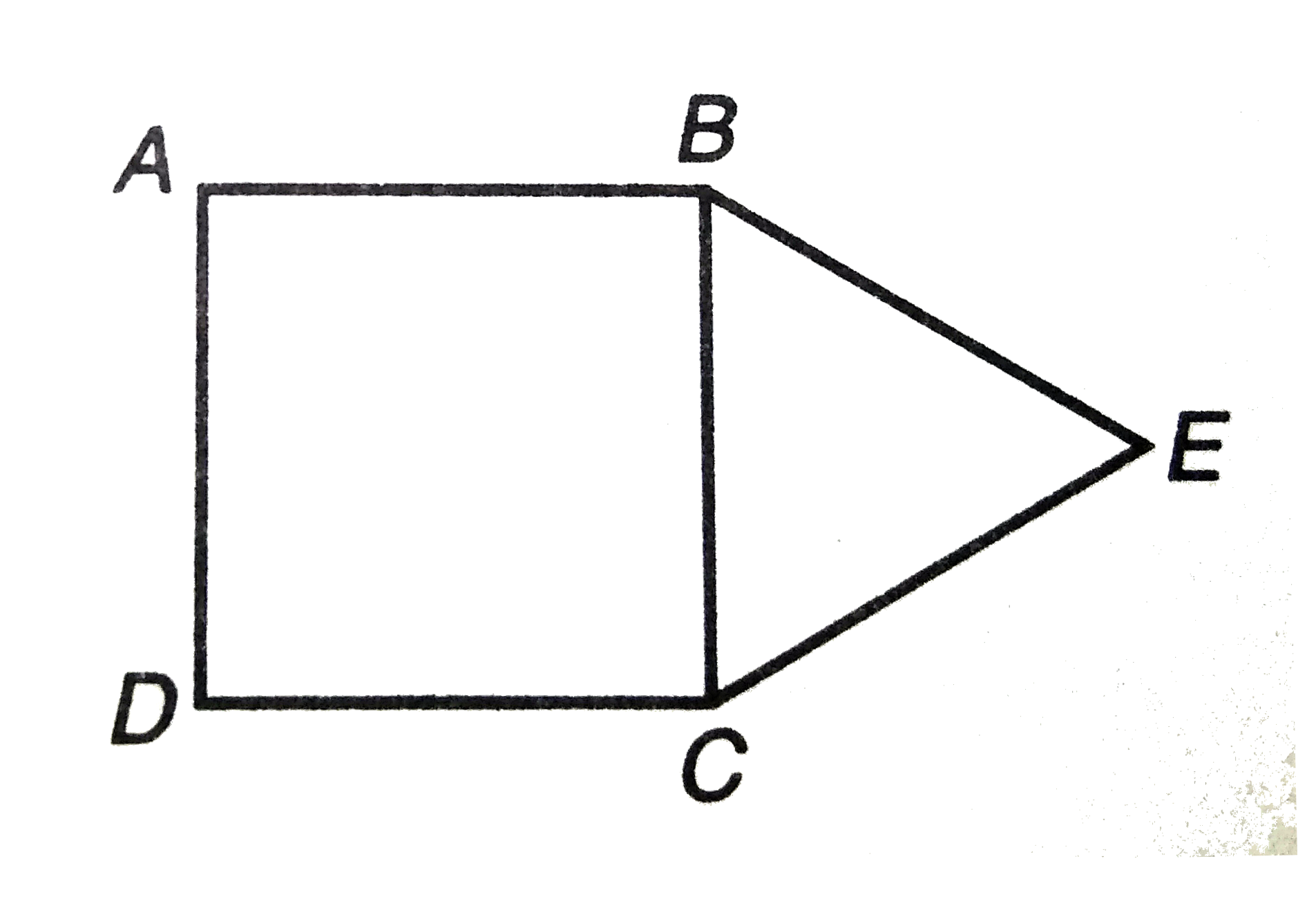
In the figure above, if the area of square ABCD is 64. What is the area equilateral triangle BEC?View Solution

