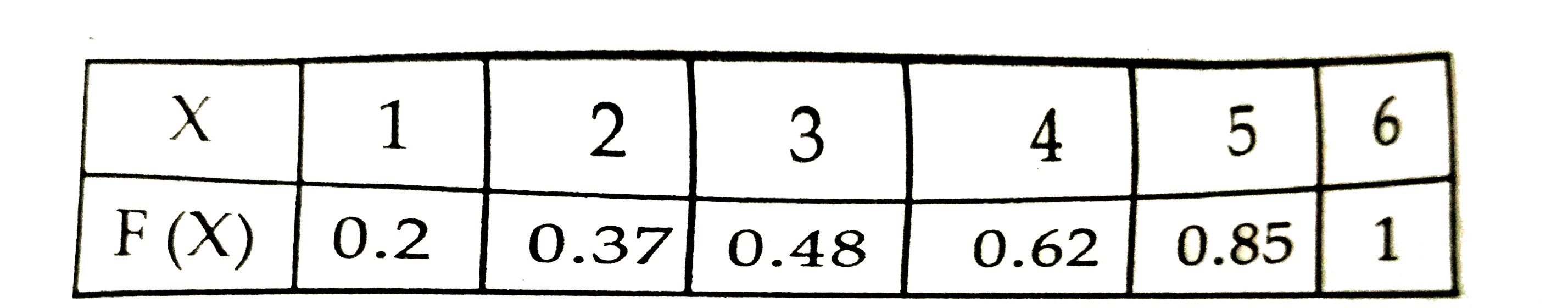For the following probability density function (p.d.f) of X find : (i) P (X<1),(ii)p(|X|<1) if f(x)=x218'−3<x<3, f(x) = 0 , otherwise
(i) p(X<1)=∫1−3f(x)=∫1−3x218=118[x33]1−3
=154[1+27]=2854=1427
(ii) P|X|<1=P(−1<x<1)
=∫1−1f(x)dx=∫1−1x218dx
=118[x33]1−1=154[1+1]
254=127
Topper's Solved these Questions
- MARCH 2019BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2019EXERCISE - SECTION-D
13 Videos
- MARCH 2019BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2019EXERCISE - SECTION-B
10 Videos
- MARCH 2018BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2018EXERCISE - SECTION - II
20 Videos
- OCTOBER 2014BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - OCTOBER 2014EXERCISE - SECTION - II
19 Videos
Similar Questions
Knowledge Check
If the function f(x)=x23,−1<x<2
= 0 , otherwise is a p.d.f of X, then P(X<0) isA19B29C39D49
For the following p.d.f of X, find P(X<1)andP(|X|≤1) : f(x)={x+218−2<x<40otherwise
View SolutionA random variable X has the following probability distribution:

Determine (i)k,(ii)P(X<3),(iii)P(0<X<3),(iv)P(X>4).
View SolutionThe following is the p.d.f (Probability Density Function ) of a continous random variable X :
f(x)=x32,0<x<8
= 0 , otherwise
Also, find its value at x = 0.5 and 9.
View SolutionFind the local maxima and local minima of the functions:
(i) f(x)=(sinx−cosx), When 0<x<π2
(ii) f(x)=(2cosx+x), when 0<x<π
View SolutionIf f(x)= kx, 0 lt x lt 2 = 0 otherwise, is a probability density function of a random variable X , then find (i) value of k, (ii) P(1 lt x lt2).
View SolutionGiven the probability density functio (p.d.f) of a continuos random variable X as. f(x)=x23,−1<x<2
Determine the cumulative distribution function (c.d.f) X and hence find P(X<1),P(X>0),P(1<X<2).
View SolutionFind k, if the following is p.d.f or r.v.f X.
f(x)={kx2(1−x)0<x<10otherwise
View Solution