From a point on the ground, the angle of elevation of an aeroplane flying at an altitude of 500m change from 45∘ to 30∘ in 5 seconds. Find the speed of the aeroplane ( in kmph).

A

243.52 km/s

B

253.52 km/s

C

263.52 km/s

D

273.52 km/s

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Let A and B be the initial and final positions of the plane.
Given, AQ=500 m
∴BR=500m(AQ=BR)
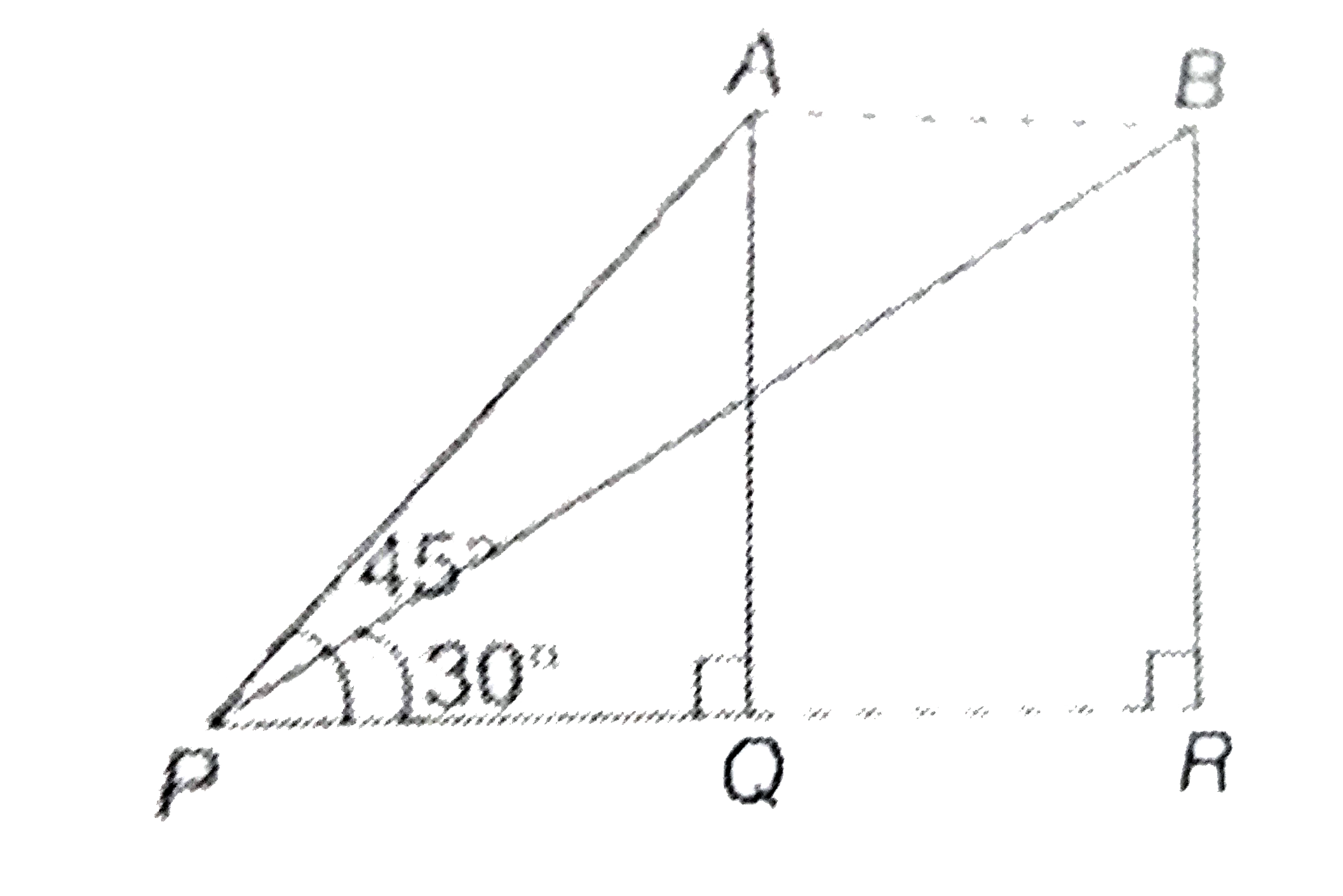
ocr_image
In ΔAPQ,
tan45∘=AQPQ
1=500pq
∴PQ = 500 m.
In ΔBPR,
tan30∘=BRPR
1√3=500PQ+QR⇒500+QR=500√3
QR=500(√3−1)m∴AB=500(√3−1)m.
Speed of the plane =ABTime
=⎛⎜ ⎜⎝500(√3−1)5⎞⎟ ⎟⎠m/s
=100(√3−1)(185)kmph
=360(√3−1)kmph

Updated on:21/07/2023
|
Class 10MATHSTRIGONOMETRIC RATIOS AND IDENTITIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • From a point on the ground, the angle of elevation of an aeroplane flying at an altitude of 500m change from 45∘ to 30∘ in 5 seconds. Find the speed of the aeroplane ( in kmph).

    A243.52 km/s
    B253.52 km/s
    C263.52 km/s
    D273.52 km/s

  • The angle of elevation of an aeroplane from a point on the ground is 60∘ .After 15 seconds flight ,the elevation changes to 30∘ .If the aeroplane is flying at a height of 1500√3 m , find the speed of the plane

    A300 m / sec
    B200 m /sec
    C100 m /sec
    D150 m/sec

  • A radar detect an aeroplane in the sky at an altitude of 5 km , at an angle of elevation of 45 .
    Find the distance of the aeroplane from the radar .

    A5√2
    B4 km
    C5 km
    D6 km