From an external point Q, the length of tangent to a circle is 12 cm and the distance of Q from the centre of circle is 13 cm. The radius of circle (in cm) is
10
5
12
7
The correct Answer is:B
To solve the problem, we will use the Pythagorean theorem. Here are the steps:
Step 1: Identify the elements of the problem
Let:
- O be the center of the circle.
- Q be the external point from which the tangent is drawn.
- P be the point of tangency on the circle.
We know:
- Length of the tangent PQ=12 cm
- Distance from point Q to the center O is OQ=13 cm
- We need to find the radius of the circle, which is OP.
Step 2: Use the Pythagorean theorem
In the right triangle OQP:
- OQ2=OP2+PQ2
Substituting the known values:
- 132=OP2+122
Step 3: Calculate the squares
Calculate 132 and 122:
- 132=169
- 122=144
Step 4: Set up the equation
Now we can set up the equation:
- 169=OP2+144
Step 5: Solve for OP2
Rearranging the equation gives:
- OP2=169−144
- OP2=25
Step 6: Find OP
Taking the square root of both sides:
- OP=√25=5 cm
Thus, the radius of the circle is 5 cm.
Final Answer:
The radius of the circle is 5 cm.
---
Let:
- O be the center of the circle.
- Q be the external point from which the tangent is drawn.
- P be the point of tangency on the circle.
- Length of the tangent PQ=12 cm
- Distance from point Q to the center O is OQ=13 cm
- We need to find the radius of the circle, which is OP.
In the right triangle OQP:
- OQ2=OP2+PQ2
- 132=OP2+122
Calculate 132 and 122:
- 132=169
- 122=144
Now we can set up the equation:
- 169=OP2+144
Rearranging the equation gives:
- OP2=169−144
- OP2=25
Taking the square root of both sides:
- OP=√25=5 cm
The radius of the circle is 5 cm.
Topper's Solved these Questions
- C.B.S.E 2020 CLASS -X (DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (DELHI)EXERCISE - DELHI SET -II ( SECTION- B )
2 Videos
- C.B.S.E 2020 CLASS -X (DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (DELHI)EXERCISE - DELHI SET -II ( SECTION- C )
3 Videos
- C.B.S.E 2020 CLASS -X (DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (DELHI)EXERCISE - DELHI SET -I ( SECTION-C )
20 Videos
- ARITHMETIC PROGRESSIONS BOOK - OSWAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - CASE - BASED MCQs
15 Videos
- C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)EXERCISE - OUTSIDE DELHI SET -III ( SECTION- D )
2 Videos
Similar Questions
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
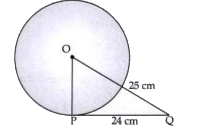
View Solution
Knowledge Check
From an external point Q, the length of the tangents to a circle is 5 cm and the distance of Q from the centre is 8 cm. The radius of the circle is:
A39 cmB3 cmC√39 cmD7 cmFrom a point Q, the length of the tangent to a circle is 12 cm and the distance of Q from the centre is 13 cm. The radius of the circle is 13 cm. The radius of the circle is :
A12 cmB13 cmC5 cmDNone of theseFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm, the radius of the circle is
A7 cmB12 cmC15 cmD24.5 cm
From a point Q, the length of the tangent to a circle is 12 cm and distance of d from the centre is 13 cm. Find the radius of the circle.
View SolutionFrom a point Q, the length of the tangent to a circle is 40 cm and the distance of Q from the center is 41 cm. The radius of the circle is ______ cm
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
View SolutionFrom a point A, the length of the tangent to ta circle is 24 cm . And the distance of a from the centre is 25 cm . The radius of the circle is
View Solution
