From the bottom of a pole of height h, the angle of elevation of the top of a tower is α. The pole subtends an angle β at the top of the tower. find the height of the tower.Solution in Bengali
hcot(α−β)cot(α−β)−cotα
htan(α−β)tan(α−β)−tanα
cot(α−β)cot(α−β)−cotα
None of these
Let AB be the tower of height H and CD be the pole
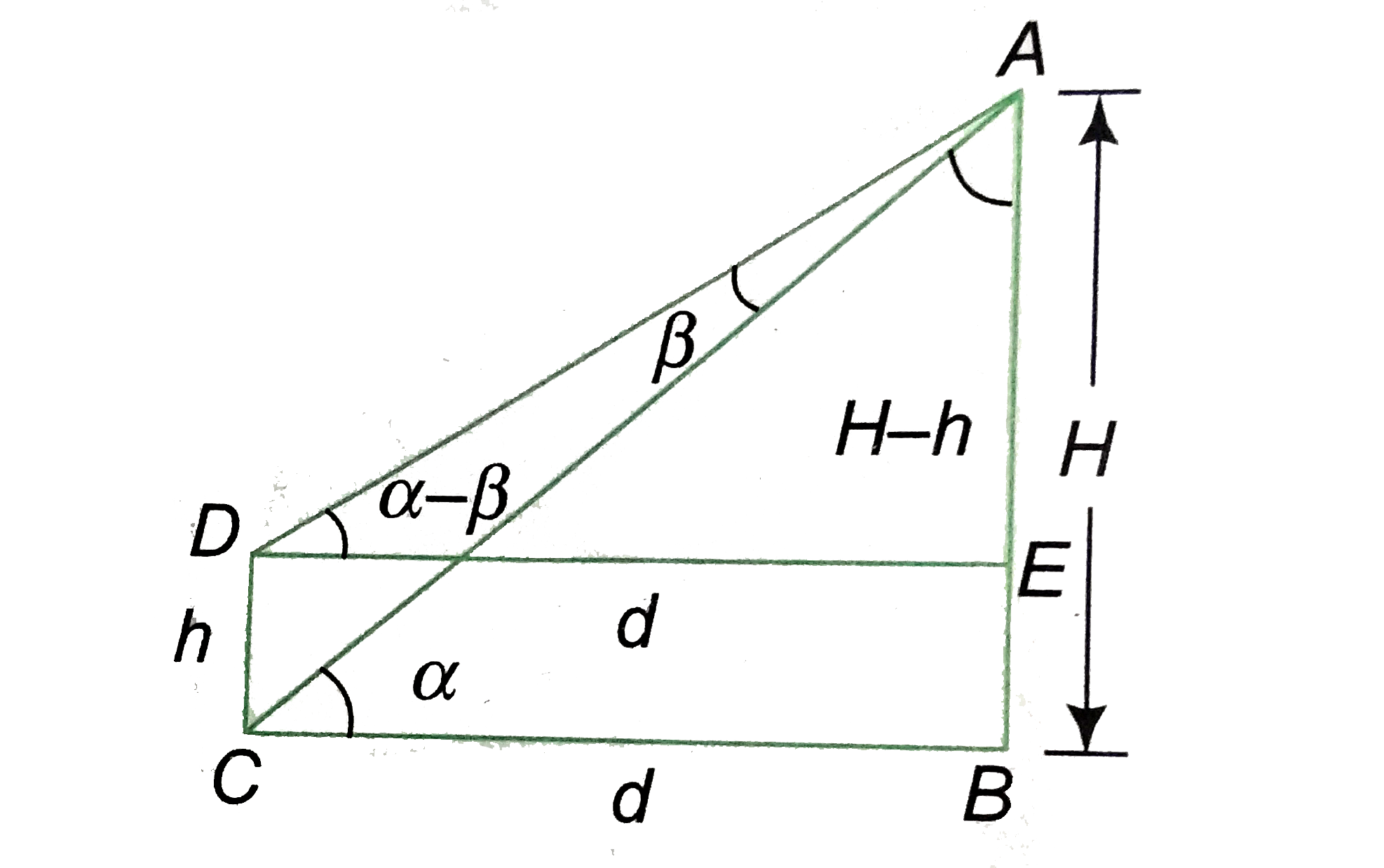
In triangle ABC, d =hcotα
In triangle AED,d =(H−h)cot(α−β)
⇒Hcotα=(H−h)cot(α−β)
∴H=hcot(α−β)cot(α−β)−cotα
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- HYPERBOLABOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE
2 Videos
Similar Questions
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
View SolutionFrom the bottom of a pole of height h,the angle of elevation of the top of a tower is alpha . The pole subtends an angle beta at the top of the tower.find the height of the tower.
View SolutionFrom te top of a tower , 60 meters high, the angles of depression of the top and bottom of a pole are αandβ respectively .Find the height of the pole.
View SolutionFrom the bottom of a pole of height h the angle of elevation of the top of a tower is alpha and the pole subtends an angle beta at the top of the tower . Prove that the height of the tower is (h cot(alpha - beta))/(cot(alpha - beta) - cot alpha) .
View SolutionAt a point on a level plane a vertical tower subtends an angle α and a pole of height a meters at the top of the tower subtends an angle β. Show that the height of the tower is a sinα cosec βcos(α+β).
View SolutionFrom the bottom of a pole of height h, the angle of elevation of the top of the tower is α. The pole subtends an angle β at the top of the tower. Prove that the height of the tower is h sinα cosec βcos(α−β)
View SolutionFrom the top and bottom of a building of height h metres, the angles of elevation of the top of a tower are αandβ respectively. Then the height of the tower is :
View SolutionFrom the top of a tower 50 m high, the angle of depression of the top of a pole is 45∘ and from the foot of the pole, the angle of elevation of the top of the tower is 60∘. Find the height of the pole if the pole and tower stand on the same plane.
View SolutionFrom the bottom of a pole of height h, the angle of elevation of the top of a tower is α. The pole subtends an angle β at the top of the tower. find the height of the tower.
View Solutionh elevation angle of the top of a tower from the foot of a pillar of height alpha is. And the angle at the top of the pillar tower beta Transmits. The height of the tower
View SolutionA vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60∘ and the angle of depression of the bottom of the tower is 30∘ . Find :
the height of the tower, it the height of the pole is 20 m ,
View SolutionA vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60∘ and the angle of depression of the bottom of the tower is 30∘ . Find :
the height of the pole, if the height of the tower is 75 m
View Solution
