Question

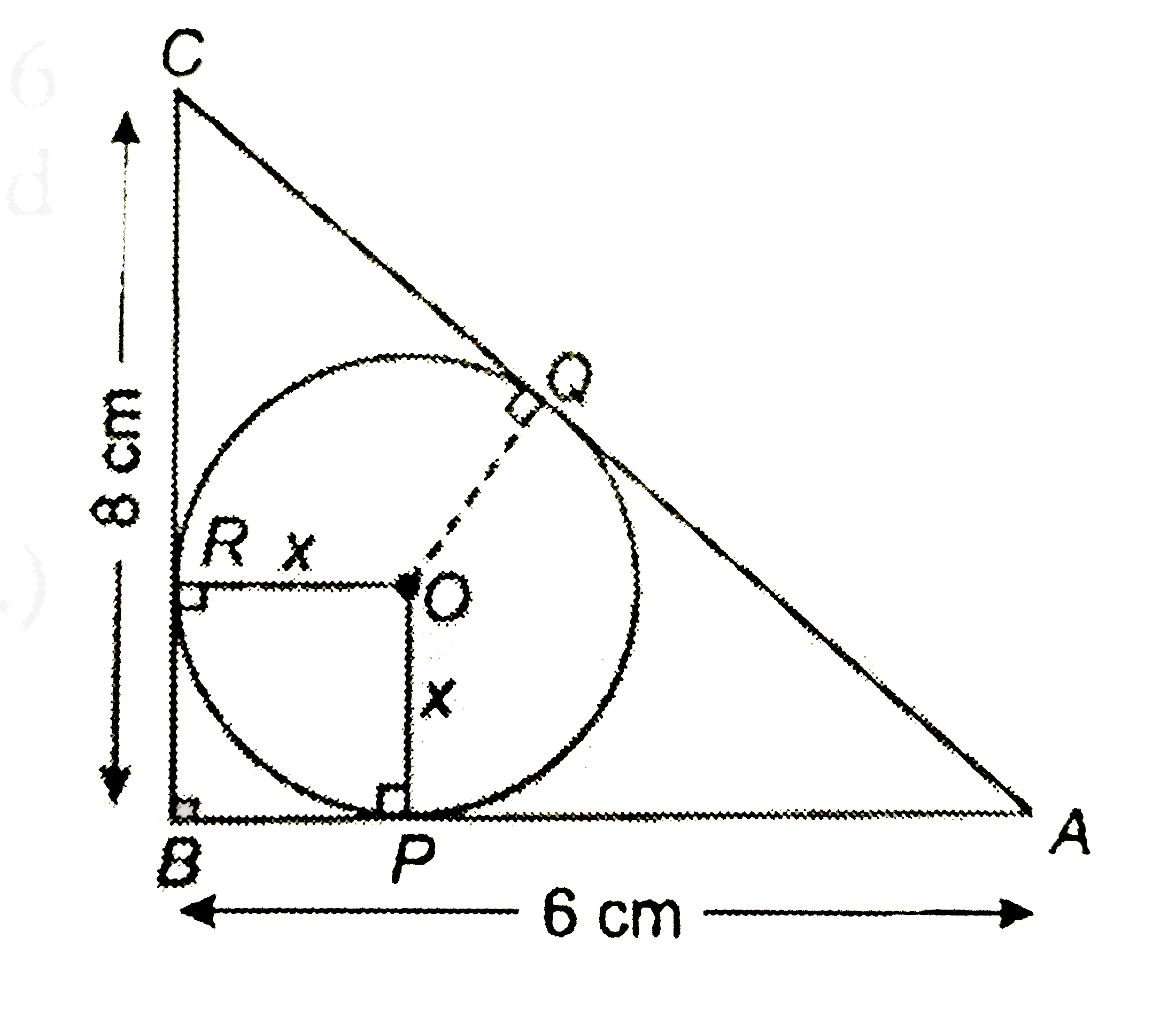
Given a right angled $△ABC$. The lengths of the sides containing the right angle are 6 cm and 8 cm. A circule is inscribed in $△ABC$. Find th radius of the circle.

Answer

2 cm

Explanation

To find the radius of the inscribed circle (inradius) of the right-angled triangle ABC with sides containing the right angle measuring 6 cm and 8 cm, we can follow these steps:

Step 1: Identify the sides of the triangle
We have a right-angled triangle ABC where:
- AB = 6 cm (one side containing the right angle)
- AC = 8 cm (the other side containing the right angle)

Step 2: Calculate the length of the hypotenuse
Using the Pythagorean theorem:
\( BC^2 = AB^2 + AC^2 \)
Substituting the values:
\( BC^2 = 6^2 + 8^2 = 36 + 64 = 100 \)
Taking the square root:
\( BC = \sqrt{100} = 10 \text{ cm} \)

Step 3: Calculate the semi-perimeter of the triangle
The semi-perimeter (s) of triangle ABC is calculated as:
\( s = \frac{AB + AC + BC}{2} = \frac{6 + 8 + 10}{2} = \frac{24}{2} = 12 \text{ cm} \)

Step 4: Calculate the area of the triangle
The area (A) of triangle ABC can be calculated using the formula for the area of a right triangle:
\( A = \frac{1}{2} \times AB \times AC = \frac{1}{2} \times 6 \times 8 = \frac{48}{2} = 24 \text{ cm}^2 \)

Step 5: Calculate the radius of the inscribed circle
The radius (r) of the inscribed circle is given by the formula:
\( r = \frac{A}{s} \)
Substituting the values we calculated:
\( r = \frac{24}{12} = 2 \text{ cm} \)

Final Answer
The radius of the inscribed circle in triangle ABC is 2 cm.

---