ABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
To find the radius of the inscribed circle (inradius) in triangle ABC, which is a right-angled triangle with sides containing the right angle measuring 6 cm and 8 cm, we can follow these steps:
1. Identify the sides of the triangle:
- Let side AB = 6 cm (one leg)
- Let side AC = 8 cm (the other leg)
- Since it's a right triangle, we can find the hypotenuse (BC) using the Pythagorean theorem.
2. Calculate the length of the hypotenuse (BC):
- According to the Pythagorean theorem:
BC=√AB2+AC2=√62+82=√36+64=√100=10 cm
3. Calculate the area of the triangle:
- The area (A) of a right triangle can be calculated using the formula:
A=12×base×height=12×6×8=24 cm2
4. Calculate the semi-perimeter (s) of the triangle:
- The semi-perimeter is calculated as:
s=AB+AC+BC2=6+8+102=242=12 cm
5. Calculate the inradius (r):
- The inradius can be calculated using the formula:
r=As=2412=2 cm
Final Answer
The radius of the inscribed circle (inradius) is 2 cm.
- Let side AB = 6 cm (one leg)
- Let side AC = 8 cm (the other leg)
- Since it's a right triangle, we can find the hypotenuse (BC) using the Pythagorean theorem.
- According to the Pythagorean theorem:
BC=√AB2+AC2=√62+82=√36+64=√100=10 cm
- The area (A) of a right triangle can be calculated using the formula:
A=12×base×height=12×6×8=24 cm2
- The semi-perimeter is calculated as:
s=AB+AC+BC2=6+8+102=242=12 cm
- The inradius can be calculated using the formula:
r=As=2412=2 cm
The radius of the inscribed circle (inradius) is 2 cm.
Topper's Solved these Questions
Similar Questions
Given a right angled △ABC. The lengths of the sides containing the right angle are 6 cm and 8 cm. A circule is inscribed in △ABC. Find th radius of the circle.
View SolutionIf the length of sides of right angled triangle are in AP, then their ratio is
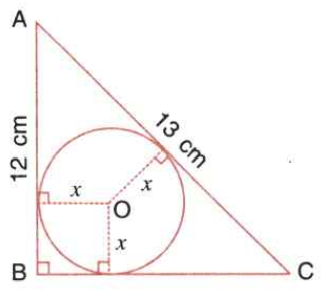
View SolutionABC is a right angled triangle with AB=12 cm and AC=13 cm. A circle, with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
View SolutionABC is a triangle right angled at C. If AB=25cmandAC=7cm, find BC.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
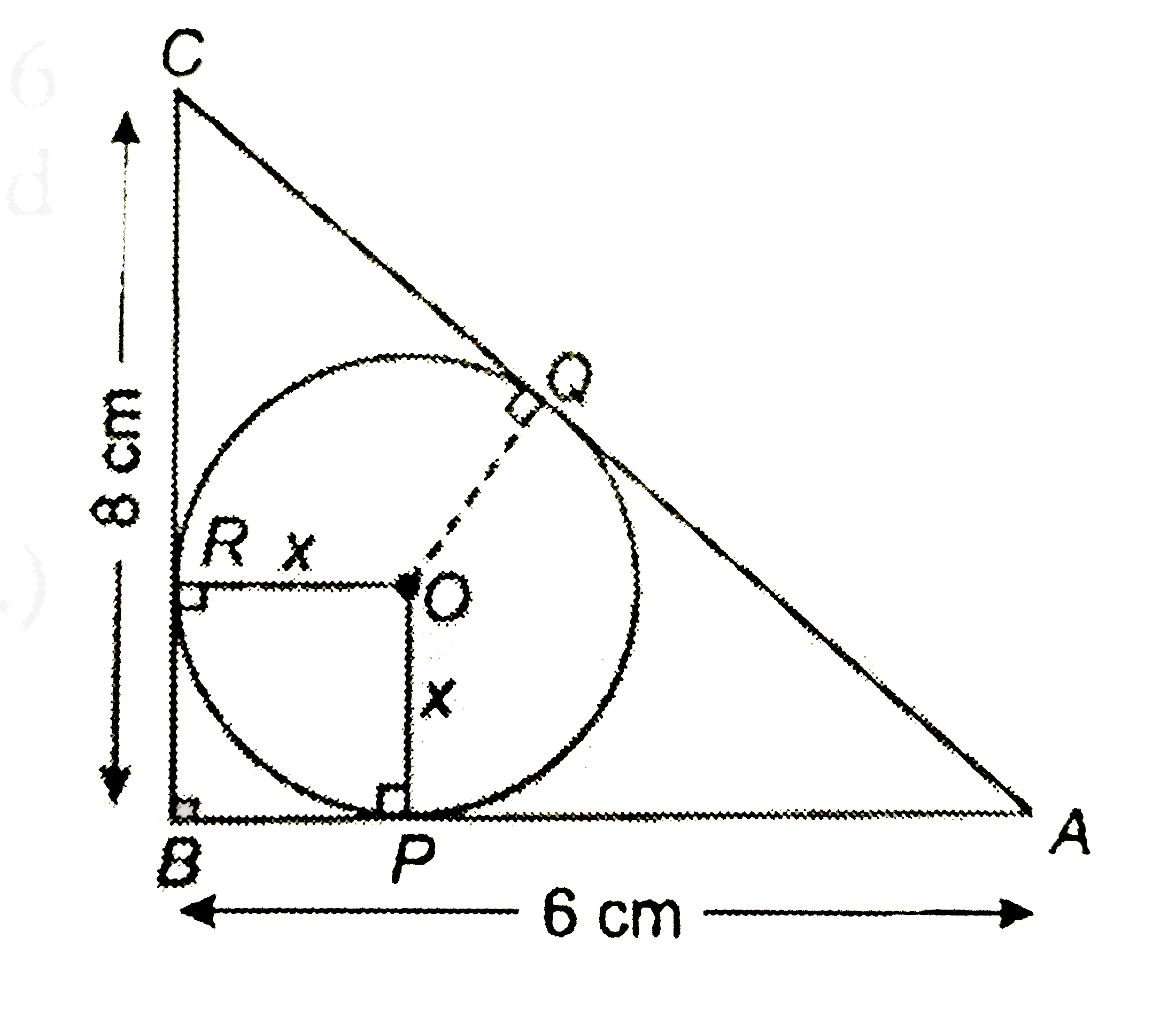
View SolutionIn the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
View SolutionA right angled isosceles triangle is inscribed in the circle x2+y2−4x−2y−4=0 then length of the side of the triangle is
View SolutionABC is a right angled triangle, right angled at B such that BC=6cm and AB=8cm . A circle with centre O is inscribed in ABC . The radius of the circle is (a) 1cm (b) 2cm (c) 3cm (d) 4cm
View SolutionIf a right angled triangle ABC of maximum Δ area is inscribed in a circle of radius R , then
View Solution
