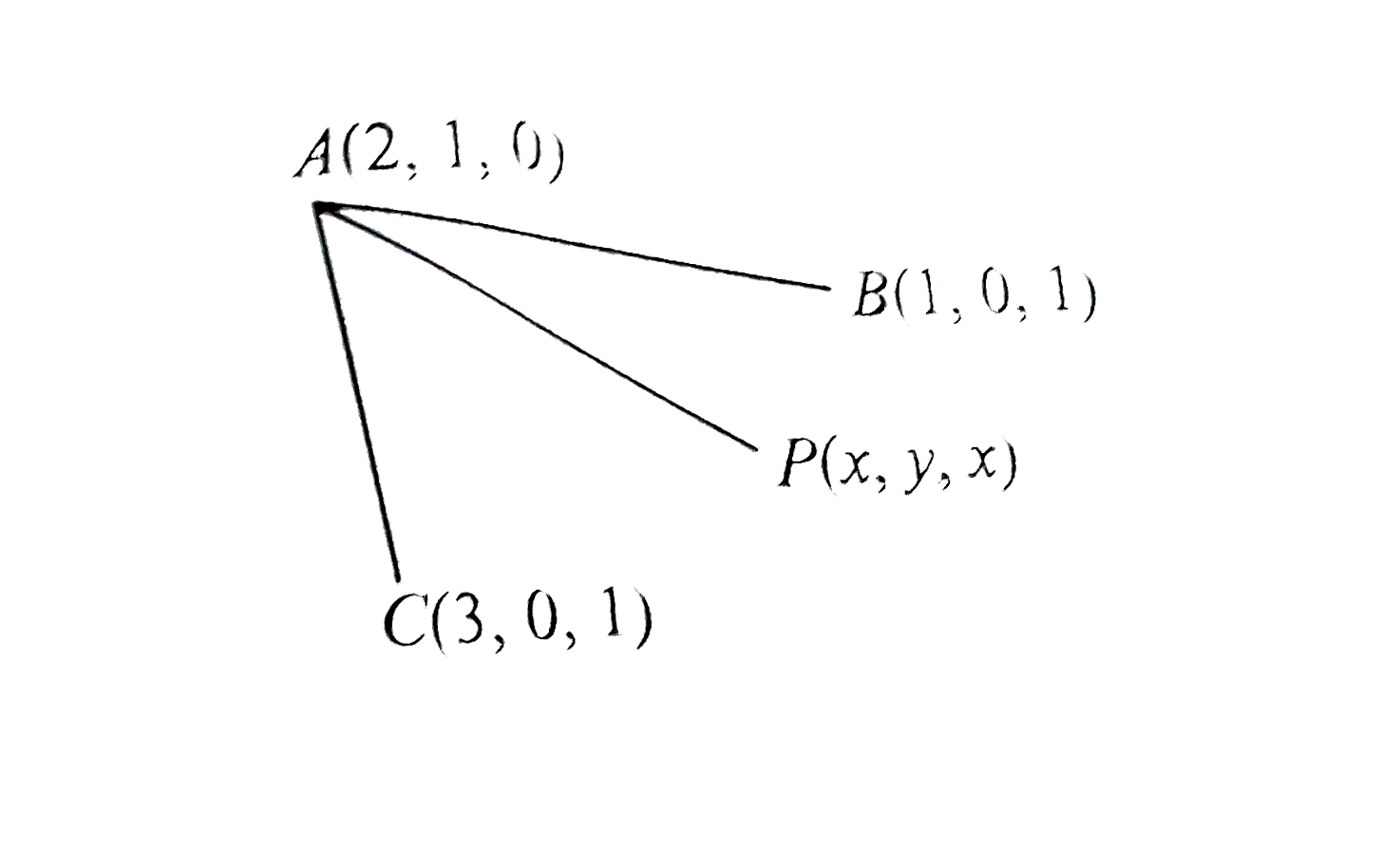
Given four points $A (2, 1, 0), B (1, 0, 1), C (3, 0, 1) and D (0, 0, 2)$ . Point D lies on a line L orthogonal to the plane determined by the points A, B and C.
The equation of the plane ABC is Solution in Bengali

A

$\to r = 2 ˆ k + λ (ˆ i + ˆ k)$

B

$\to r = 2 ˆ k + λ (2 ˆ j + ˆ k)$

C

$\to r = 2 ˆ k + λ (ˆ j + ˆ k)$

D

none

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c

$∣ ∣ ∣ ∣ ∣ \begin{matrix} x - 2 & y - 1 & z 1 - 2 & 0 - 1 & 1 - 0 3 - 2 & 0 - 1 & 1 - 0 \end{matrix} ∣ ∣ ∣ ∣ ∣ = 0$
$(x - 2) [(- 1) - (- 1)] - (y - 1) [(- 1) - 1] + z [1 + 1] = 0$
or $2 (y - 1) + 2 z = 0$
or $y + z - 1 = 0$
The vector normal to the plane is $\to r = 0 ˆ i + ˆ j + ˆ k$
The equation of the line through $(0, 0, 2)$ and parallel to $\to n$ is $\to r = 2 ˆ k + λ (ˆ j + ˆ k)$
The perpendicular distance of $D (0, 0, 2)$ from plane
$A B C$ is $∣ ∣ ∣ ∣ ∣ \frac{2 - 1}{\sqrt{1^{2} + 1^{2}} ∣ = \frac{1}{\sqrt{2}}}$

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-THREE-DIMENSIONAL GEOMETRY -LINKED COMPREHENSION TYPE

Home
Ask Doubt
Profile