Given : In trapezium PQRS, side PQ||SR, AR = 5 AP, AS = 5 AQ, then prove that SR=5 PQ.
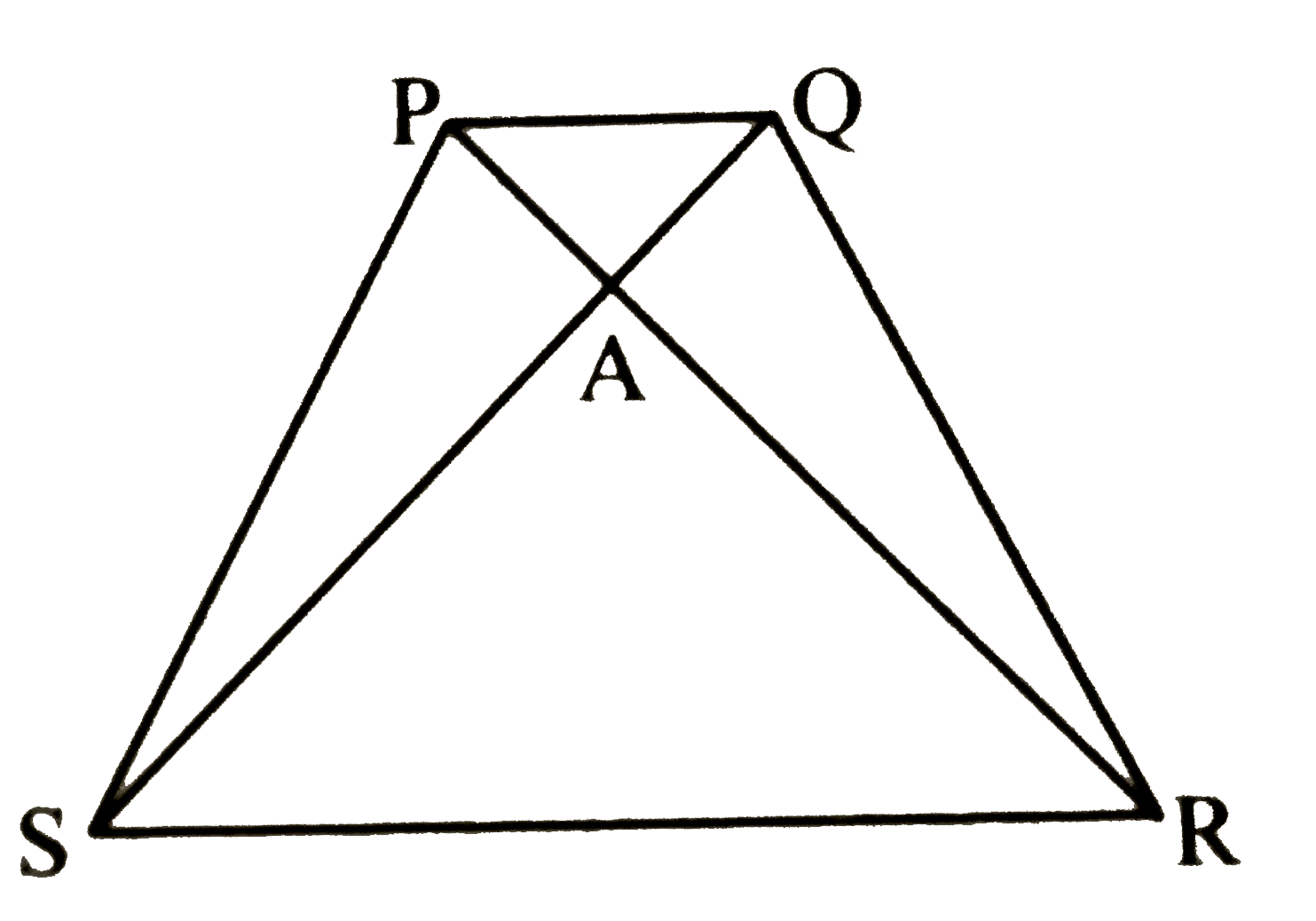
The correct Answer is:∴ SR = 5 PQ
Step by step video & image solution for Given : In trapezium PQRS, side PQabs()SR, AR = 5 AP, AS = 5 AQ, then prove that SR=5 PQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Practice Set 1.4
7 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Problem Set - 1
19 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Practice Set 1.2
11 Videos
- QUESTION FROM STD. IXBOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics
14 Videos
- STATISTICSBOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-6
21 Videos
Similar Questions
Given : In trapezium PQRS,sPQ∣∣sSR,AR=5AP,AS=5AQthen prove that,SR=5PQ
View SolutionGiven: In trapezium PQRS, sides PQ∣∣ sides SR,AR=5AP,AS=5AQ, then prove that SR=5PQ.
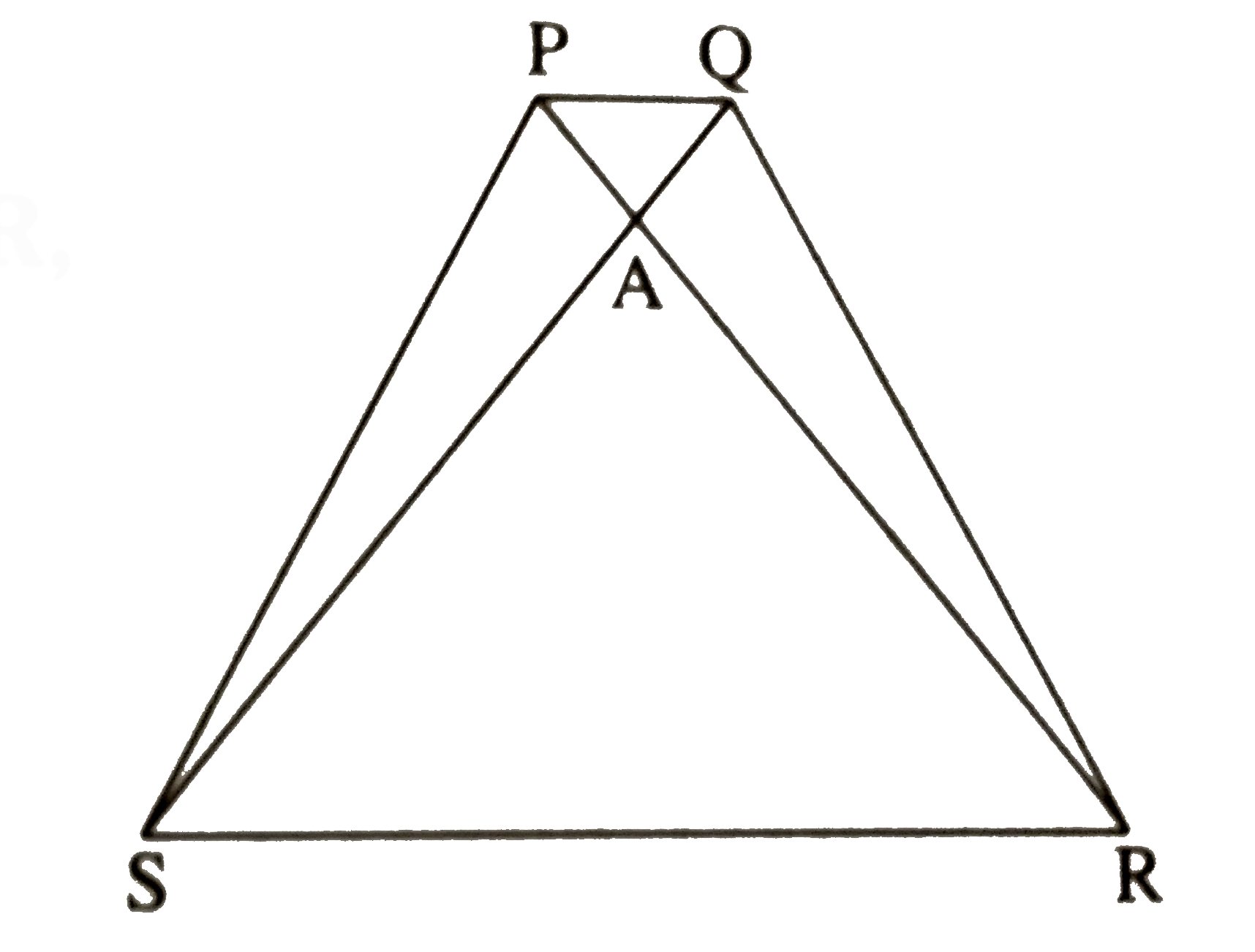
View SolutionIn trapezium PQRS, side PQ∣∣ side SR, AR=5AP, AS=5AQ then prove that SR=5PQ by completing the following activity.
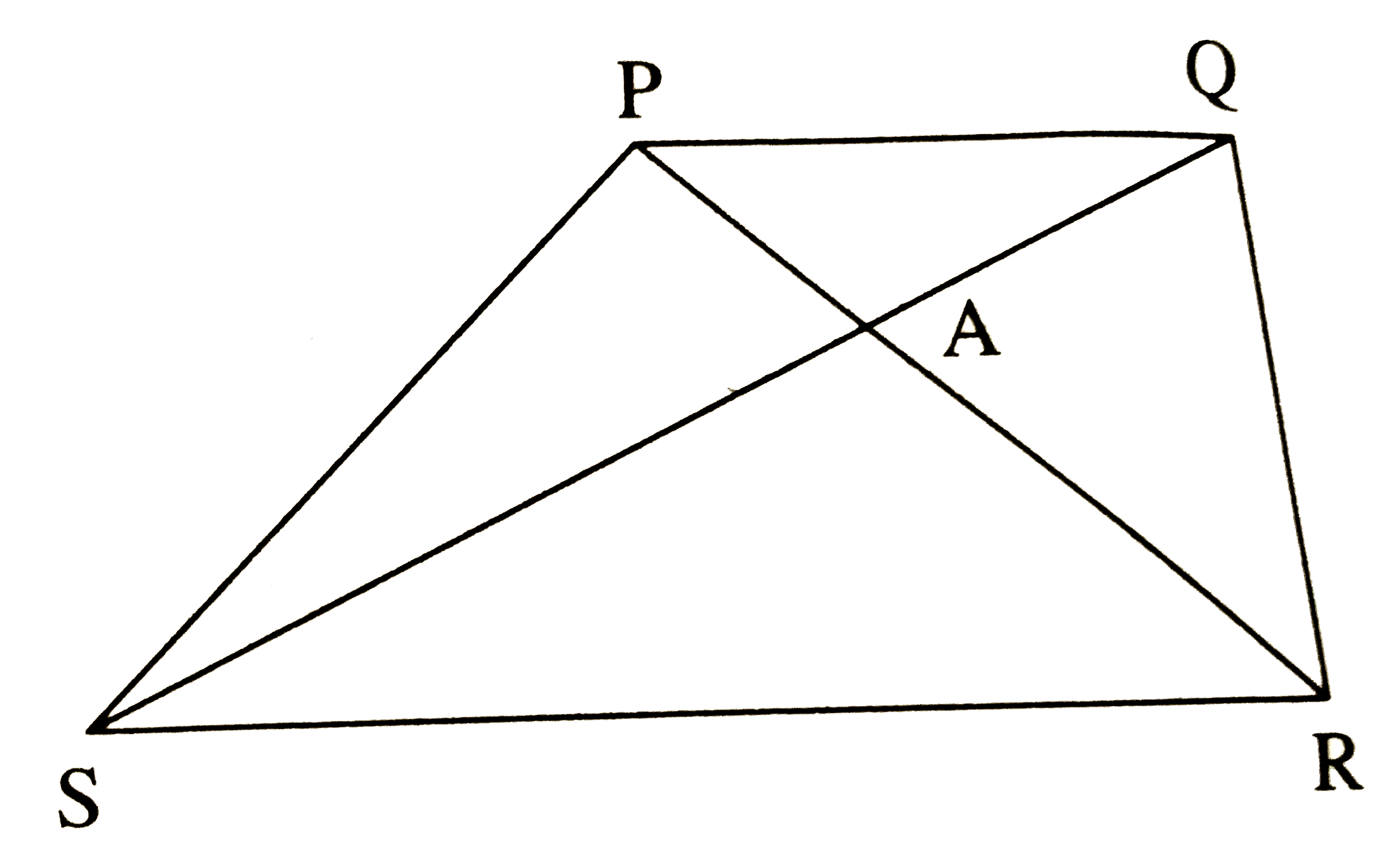
In ΔPQA and ΔRSA,
∠PQA≅∠RSA……(□)
∠PAQ≅∠RAS....(□)
∴ΔPQA~ΔRSA ......(□)
PQSR=□AR.........(Corresponding sides of similar triangles).....(1)
Substituting AR=5AP in (1)
∴PQSR=□5AP
∴PQSR=□5
∴SR=5PQ
View Solution∠PQR=∠PRS, then prove that ∠PQS=∠PRT
View SolutionIn trapezium PQRS,side PQ∣∣ sideSR. Diagonals PR and QS intersect each other at point M. PQ=2RS. Prove that PM=2RM and QM=2SM.
View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
View SolutionIf Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View SolutionIn the given figures, if PQRS is a parallelogram and AB||PS, then prove that OC||SR.
View SolutionIn trapezium PQRS, PQ || SR and the ratio of PQ to SR is 3:2. If the area of the trapezium is 480cm2 and the distance between PQ and SR is 12 cm, then the length of SR is
View SolutionIn a trapezium PQRS, PQ||SR and PQ= 2 SR. if the diagonals intersect at O and area of △POQ=96cm2 , find th area of △SOR.
View Solution
