Given points P(2,3),Q(4,−2),andR(α,0). Find the value of α if PR+RQ is minimum.Solution in Bengali
(i) Point R(α,0) lies on x-axis.
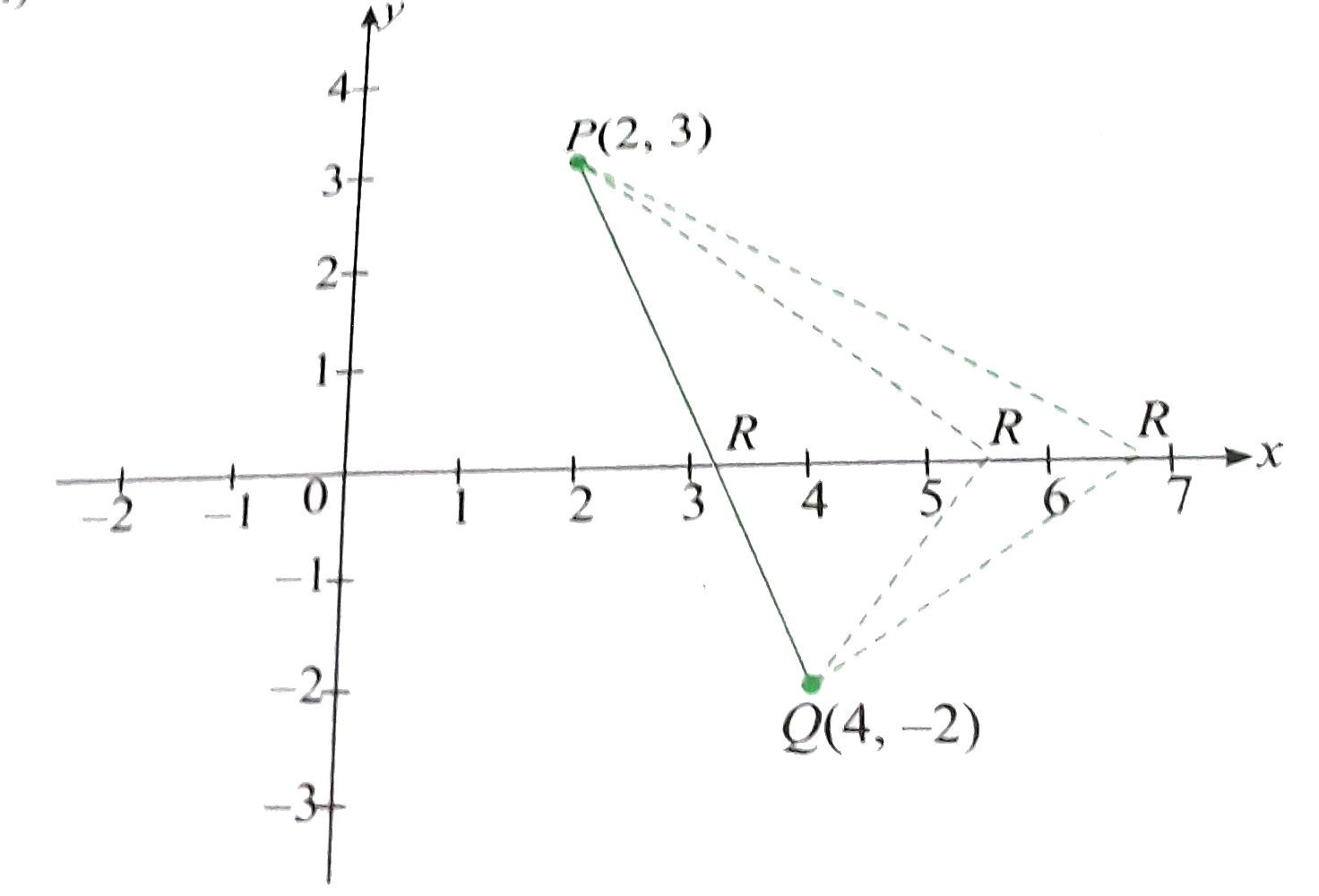
Now, from triangular inequality, PR+RQ≥PQ
Thus minimum value of PR+RQ is PQ, which occurs when points P,Q and R are collinear.
⇒∣∣
∣
∣
∣∣234−2α023∣∣
∣
∣
∣∣=0
⇒−4−12+2α+3α=0
⇒α=16/5
(ii) 
Image of Q in x-axis is Q'(4,2).
Now, RQ=RQ'
∴|PR−RQ|=|PR−RQ'|
From triangle inequality,
|PR−PQ'|≤PQ'.
∴|PR−PQ'|max=PQ', when P,Q' and R are collinear
∴∣∣
∣
∣
∣∣2342α023∣∣
∣
∣
∣∣=0
⇒4−12−2α+3α=0
⇒α=8
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.221videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.231videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.201videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
If A(3√2,√2), B(−3√2,√2),C(−3√2,−√2) and D(3cosθ,2sinθ) are four points . If the area of the quadrilateral ABCD is maximum where θ∈(3π2,2π) then (a) maximum area is 10 sq units (b) θ=7π4 (c) θ=2π−sin−13√85 (d) maximum area is 12 sq units
09:16View SolutionFind the coordinates of the point which divides the line segments joining the points (6,3) and (−4,5) in the ratio 3:2 (i) internally and (ii) externally.
05:16View SolutionIf the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
05:21View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
07:18View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
03:58View SolutionIf P,Q and R are three points with coordinates (1,4),(4,5) and (m,m) respectively,then the value of m for which PR+RQ is minimum,is:
05:45View SolutionGiven points P(2,3),Q(4,-2), and R(alpha,0). Find the value of a if PR+RQ is minimum.
05:53View SolutionA man strats from the point P(−3,4) and reaches the point Q(0,1) touching the x-axis at R(α,0) such that PR+RQ is minimum. Then |α|=.
01:10View SolutionIf P=(1,1),Q=(3,2) and R is a point on x-axis then the value of PR+RQ will be minimum at
07:46View SolutionIf Δ=∣∣ ∣ ∣∣0qrqrprpq∣∣ ∣ ∣∣, then ∣∣ ∣ ∣∣rq−p2pr−q2pq−r2rp−q2pq−r2rq−p2pq−r2rq−p2pr−q2∣∣ ∣ ∣∣ is equal to
08:39View SolutionGiven points P(2,3),Q(4,−2),andR(α,0) (i) Find the value of (ii)α(iii) (iv) if (v)(vi)PR+rQ(vii) (viii) is minimum (ix) Find the value of (x)α(xi) (xii) if (xiii)(ξv)|(xv)PR−RQ|(xvi) (xvii) is maximum
07:29View SolutionGiven points P(2,3),Q(4,−2),andR(α,0). Find the value of a if PR+RQ is minimum.
04:10View SolutionA man strats from the point P(−3,4) and reaches the point Q(0,1) touching the x-axis at R(α,0) such that PR+RQ is minimum. Then |α|=.
02:46View SolutionIf P=(1,1),Q=(3,2) If point R is located on the x axis, PR+RQ Value of will be minimum
04:57View SolutionIf P=(1,1),Q=(3,2) If point R is located on the x axis, PR+RQ Value of will be minimum
05:15View SolutionLet P(1,1) and Q(3,2) be given points. Find the point R on the x-axis such that PR+RQ is minimum
01:45View Solution