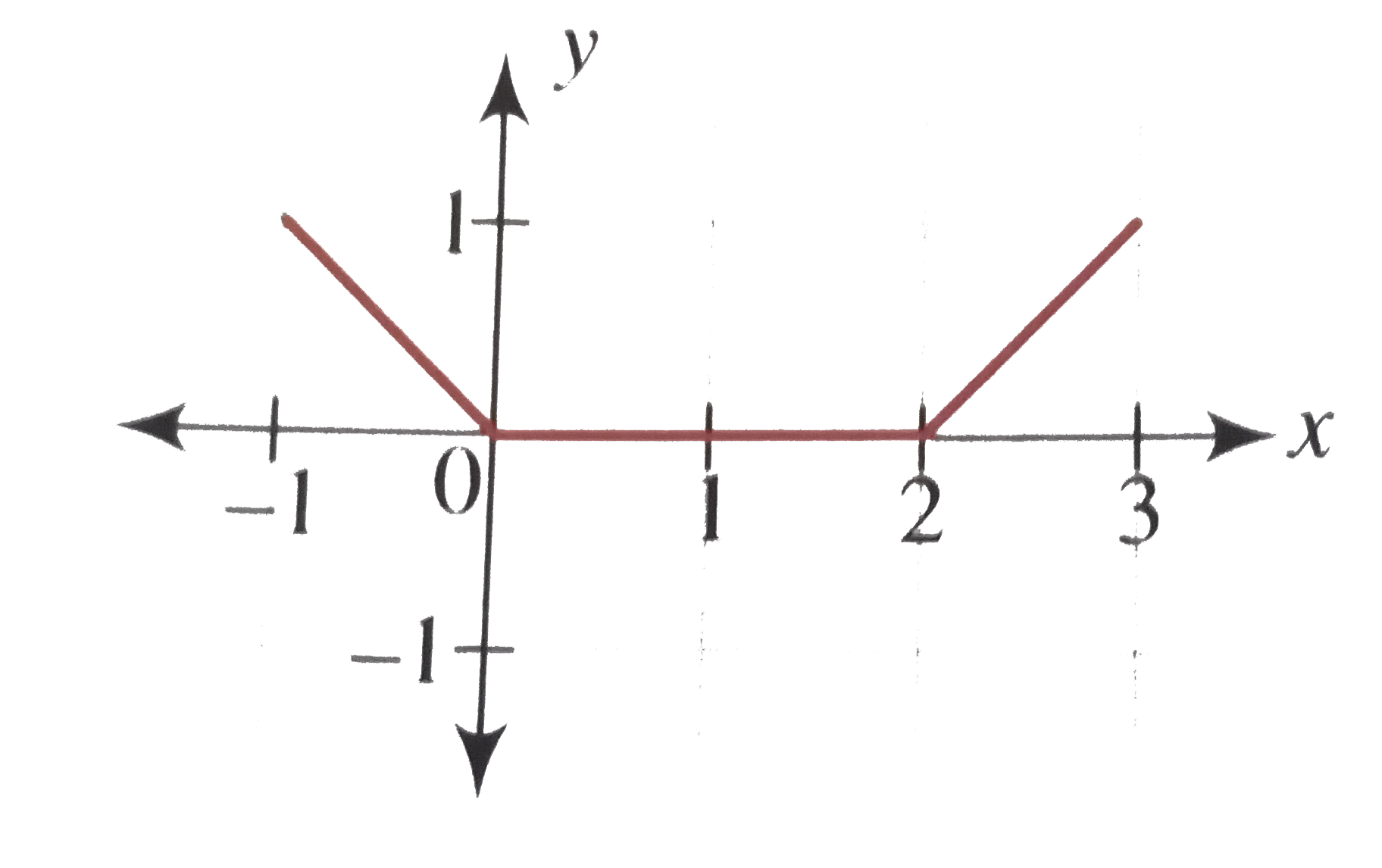
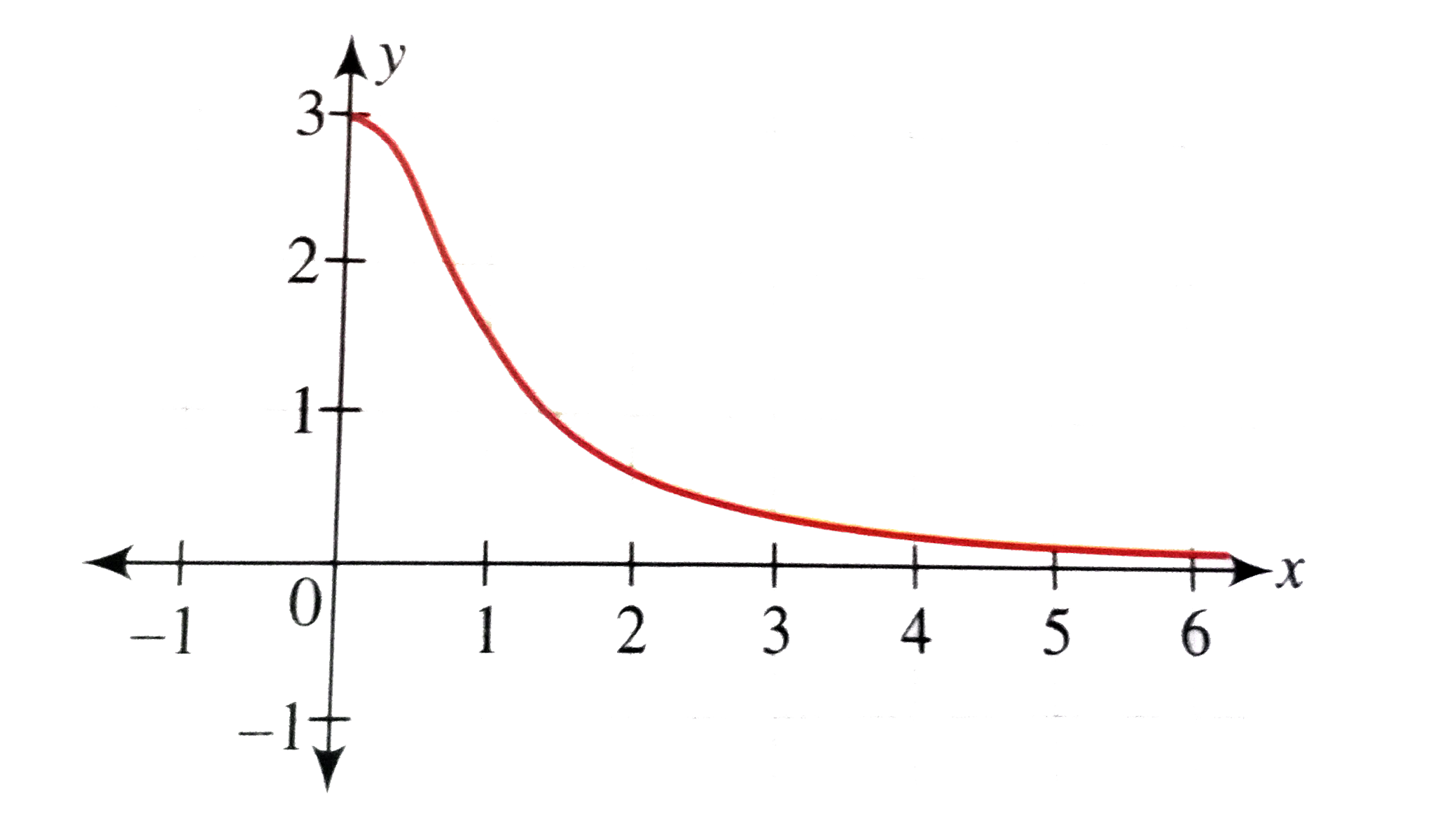
Given the graph of y=f(x).

Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
(a) y=f(1−x)
For the graph of y=f(x), flip the graph of y=f(x) over the y-axis.
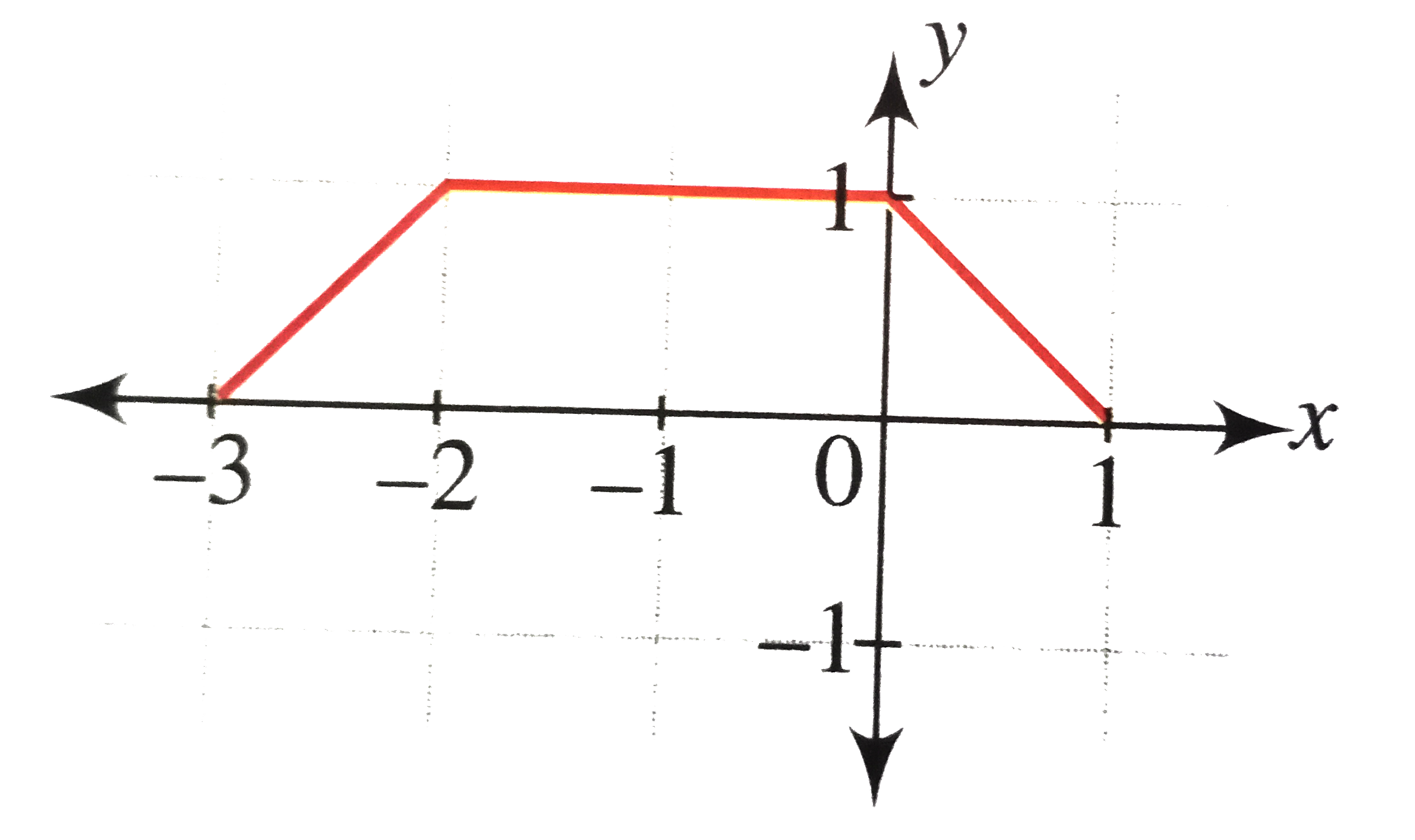
For the graphs of y=f(1−x), shift the above graph '1' units to the right horizontally.
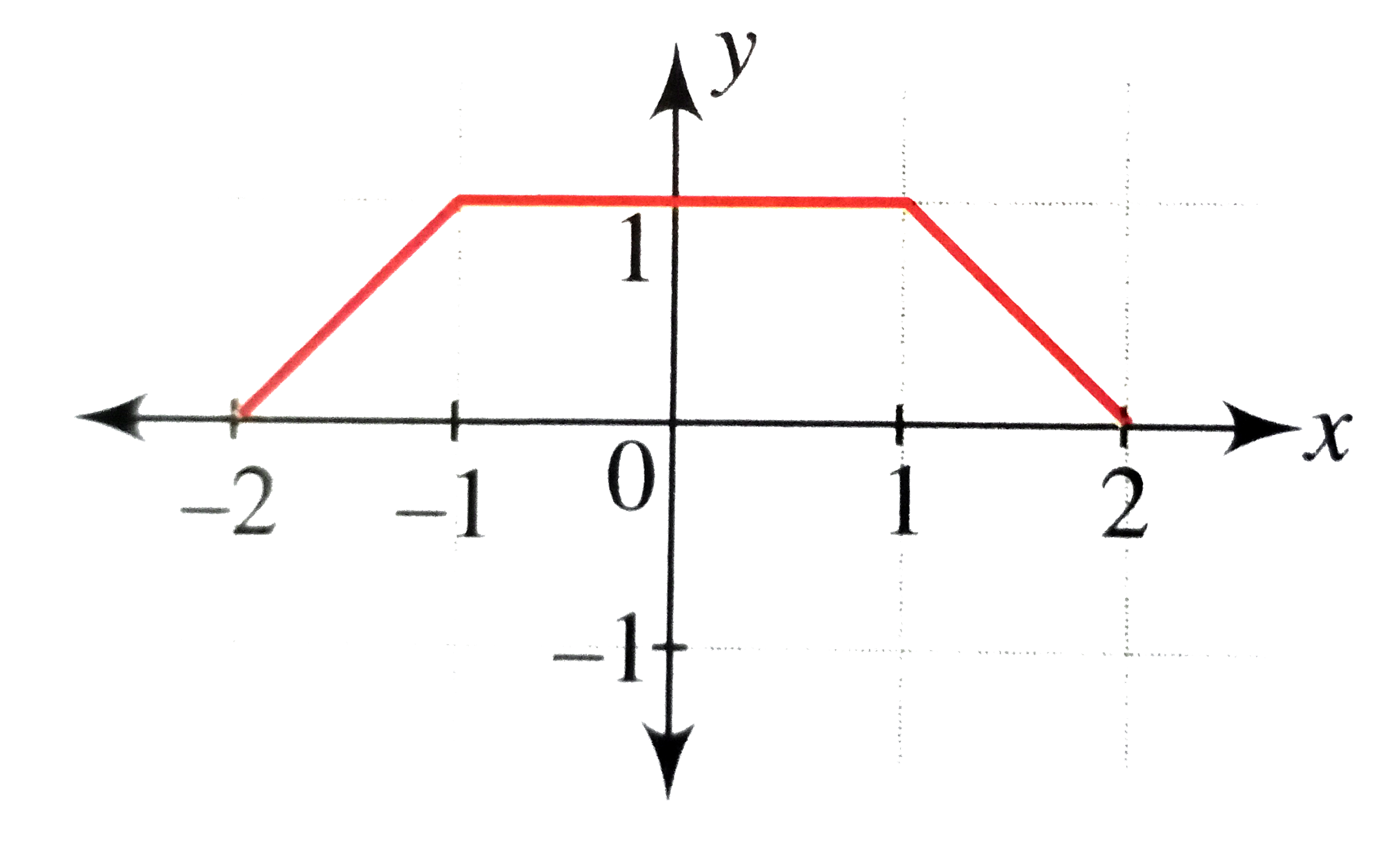
(c) y=f(2x)
For the graph of y=f(2x), compress the graph of y=f(x)'2' times horizontally.
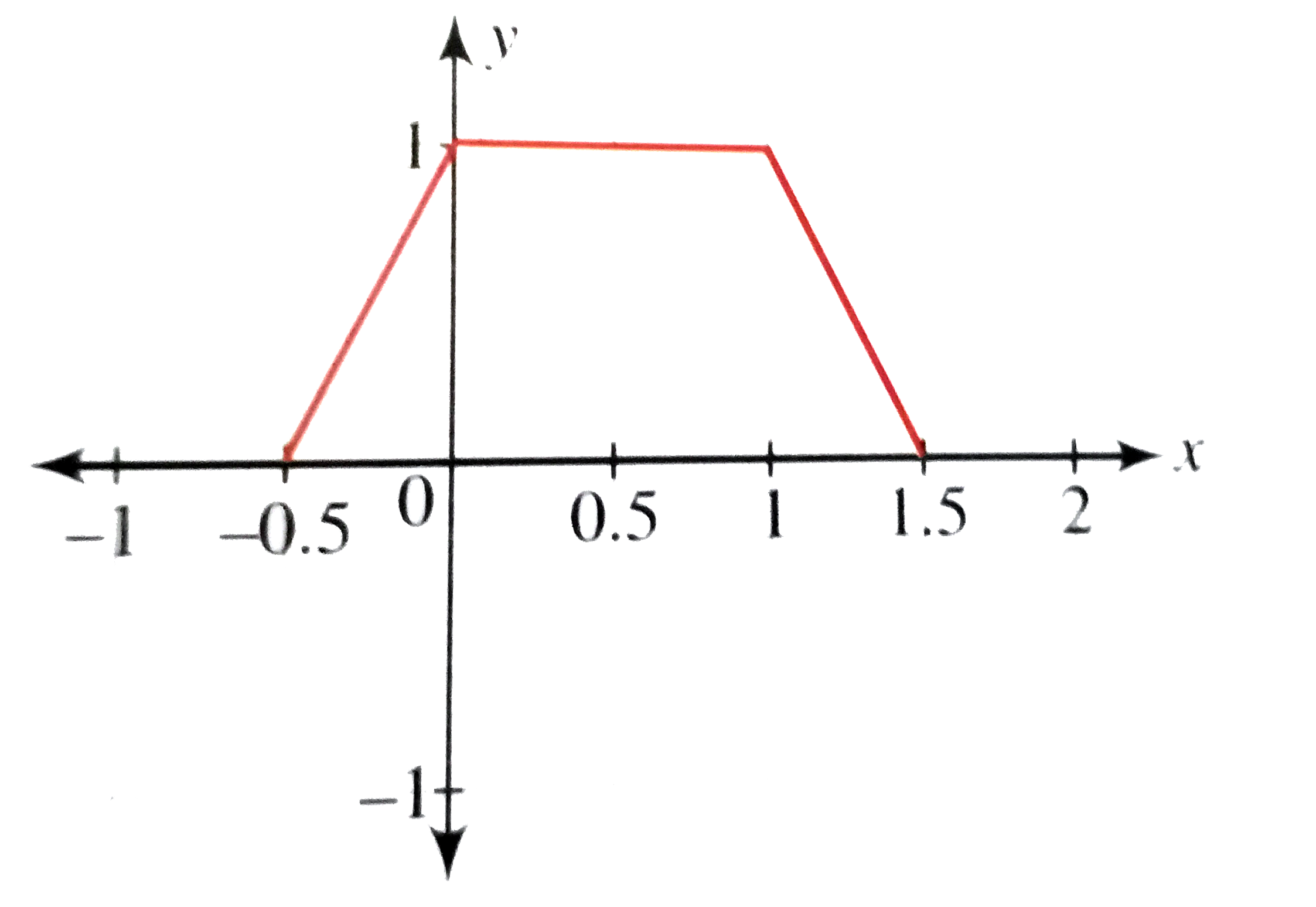
(c) y=−2f(x)
For the graph of y=2f(x), stretch the graph of y=f(x)'2' times vertically.

For the graph of y=−2f(x), flip the above graph over the x-axis.
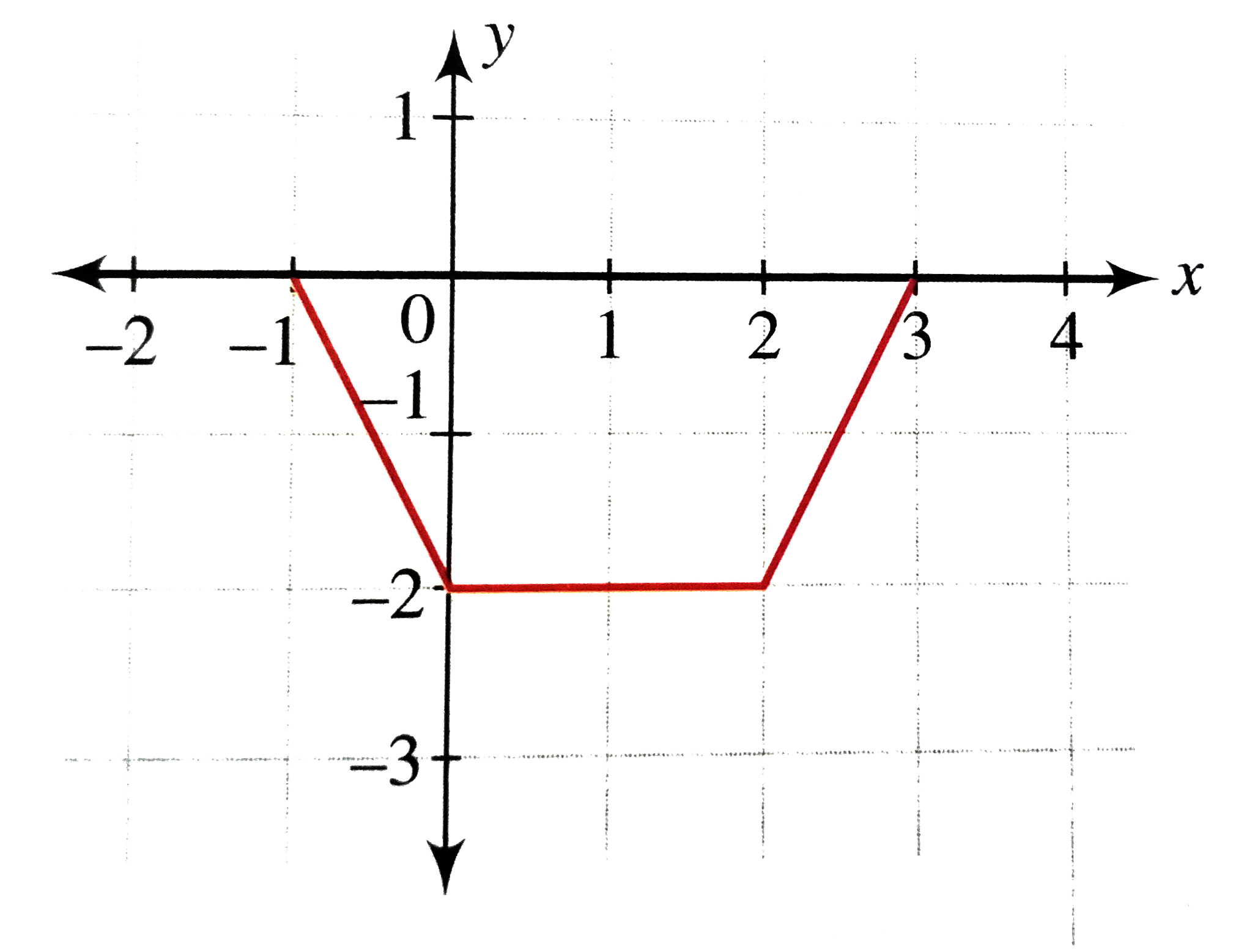
(d) y=1−f(x)
For the graph of y=−f(x), flip the graph of y=f(x) over the x-axis.

For the graph of y=1−f(x), shift the above graph by '1' unit vertically.
Topper's Solved these Questions
Similar Questions
Given the graph of y=f(x), which of the following is graph of y=f(1−x)
View SolutionGiven the graph of f(x), draw the graph each one of the following functions :
(a) y=f(x)+3 (b) y=−f(x)+2
(c ) y=f(x+1)−2 (d) y=−f(x−1)
(e ) y=f(−x) (f) y=f(|x|)
(g) y=f(1−x)
View SolutionGiven the graph of the function y=f(x), draw the graph of y=sgn(x).
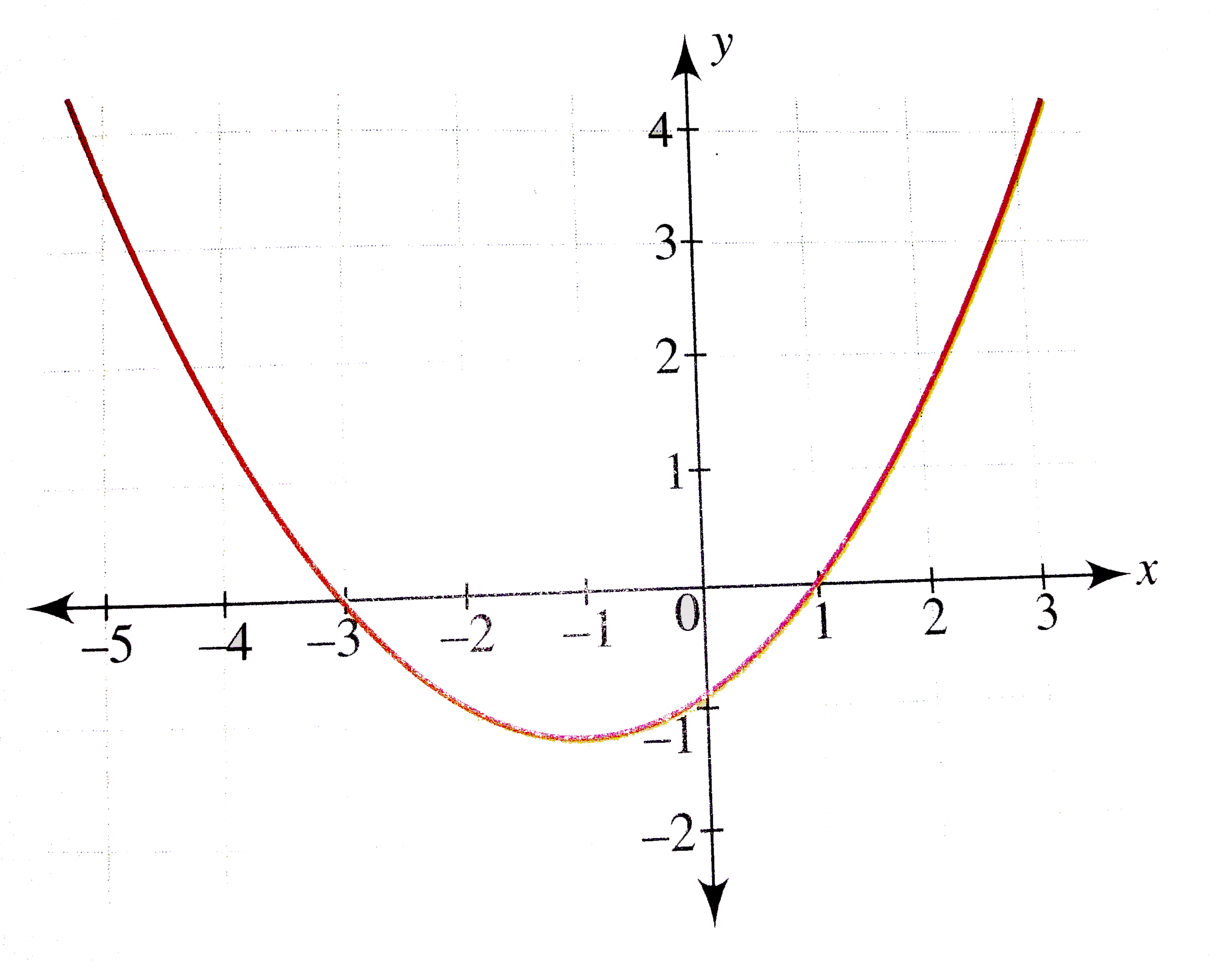
View SolutionThe graph y = f (x) is as shown:
The graph of y = f (–|x|) is:
View SolutionDraw the graph of the function y=f(x)=tan−1(1−x21+x2).
View SolutionIf the graph of y=|f(x)| is as shown in figure
 then the graph of y=f(x) may be
then the graph of y=f(x) may be
View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) is
View SolutionThe graph of y=f(x) is as shown in the following figure. Draw the graph of y=[f(x)].
View SolutionThe graph of y=f(x) is given below
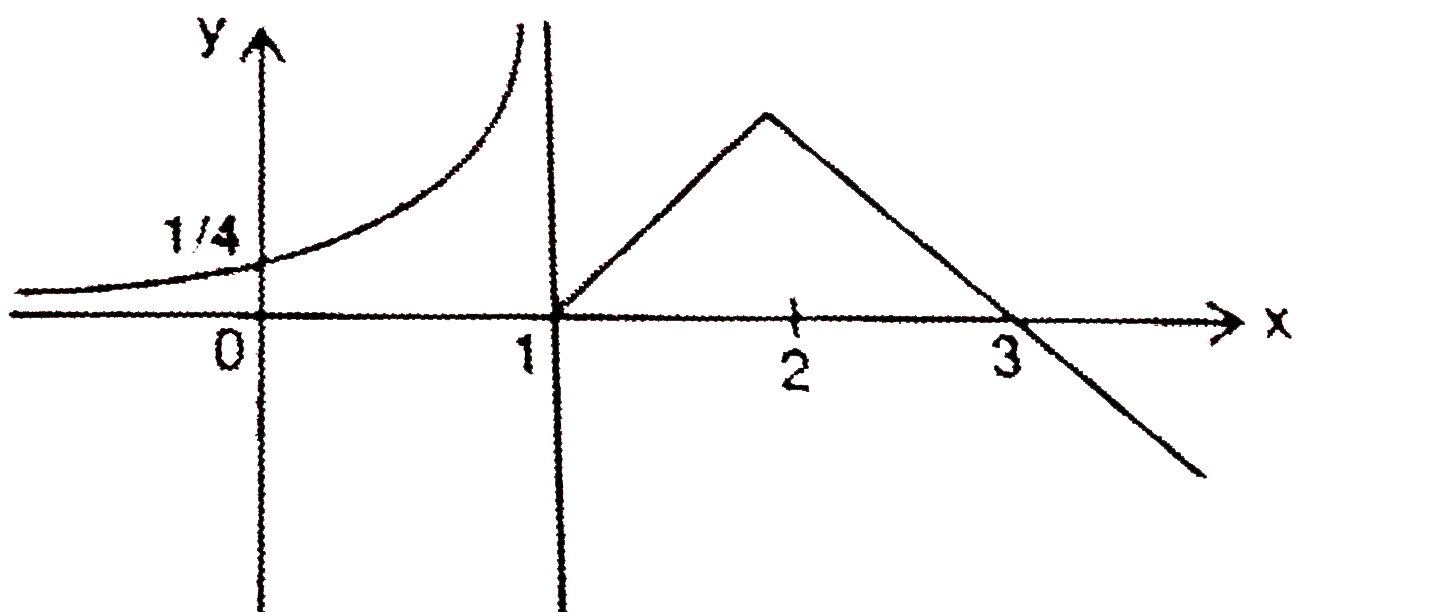
then the graph y=|f(|x|)| is :
View SolutionDraw the graph of y=f(x)=√1−cosx
View Solution
