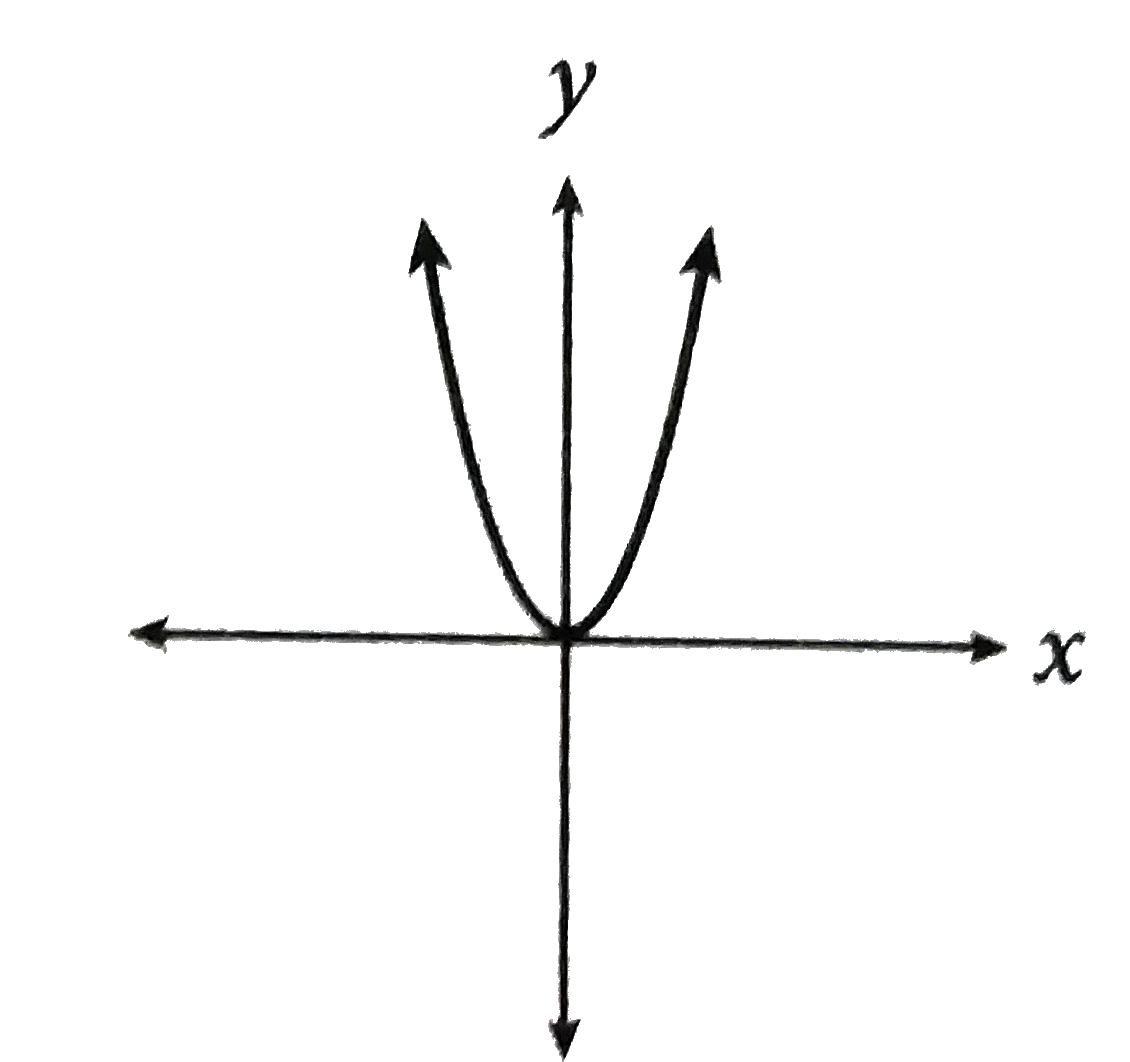
Given the graph of y=f(x), which of the following is graph of y=f(1−x)
To solve the problem of finding the graph of y=f(1−x) given the graph of y=f(x), we can follow these steps:
1. Understand the Transformation:
The expression f(1−x) indicates a transformation of the function f(x). The term 1−x suggests a reflection and a horizontal shift.
2. Horizontal Reflection:
The term −x indicates that we will reflect the graph of f(x) across the vertical line x=1. This means that for every point (a,b) on the graph of f(x), the corresponding point on the graph of f(1−x) will be (1−a,b).
3. Horizontal Shift:
The +1 in 1−x means that after reflecting, we will shift the graph to the right by 1 unit.
4. Plotting Points:
To illustrate this transformation, we can take specific points from the graph of f(x) and apply the transformation:
- If (a,f(a)) is a point on f(x), then the corresponding point on f(1−x) will be (1−a,f(a)).
- For example, if f(0)=2, then the point (0,2) on f(x) will transform to (1−0,2)=(1,2) on f(1−x).
5. Drawing the New Graph:
After applying the transformation to several key points on the graph of f(x), we can sketch the new graph of f(1−x).
6. Final Graph:
The final graph will show the reflection of the original graph across the vertical line x=1 followed by a rightward shift of 1 unit.
The expression f(1−x) indicates a transformation of the function f(x). The term 1−x suggests a reflection and a horizontal shift.
The term −x indicates that we will reflect the graph of f(x) across the vertical line x=1. This means that for every point (a,b) on the graph of f(x), the corresponding point on the graph of f(1−x) will be (1−a,b).
The +1 in 1−x means that after reflecting, we will shift the graph to the right by 1 unit.
To illustrate this transformation, we can take specific points from the graph of f(x) and apply the transformation:
- If (a,f(a)) is a point on f(x), then the corresponding point on f(1−x) will be (1−a,f(a)).
- For example, if f(0)=2, then the point (0,2) on f(x) will transform to (1−0,2)=(1,2) on f(1−x).
After applying the transformation to several key points on the graph of f(x), we can sketch the new graph of f(1−x).
The final graph will show the reflection of the original graph across the vertical line x=1 followed by a rightward shift of 1 unit.
Similar Questions
Knowledge Check
If f(x)=4x+2, which of the following is the graph of f(x)?
A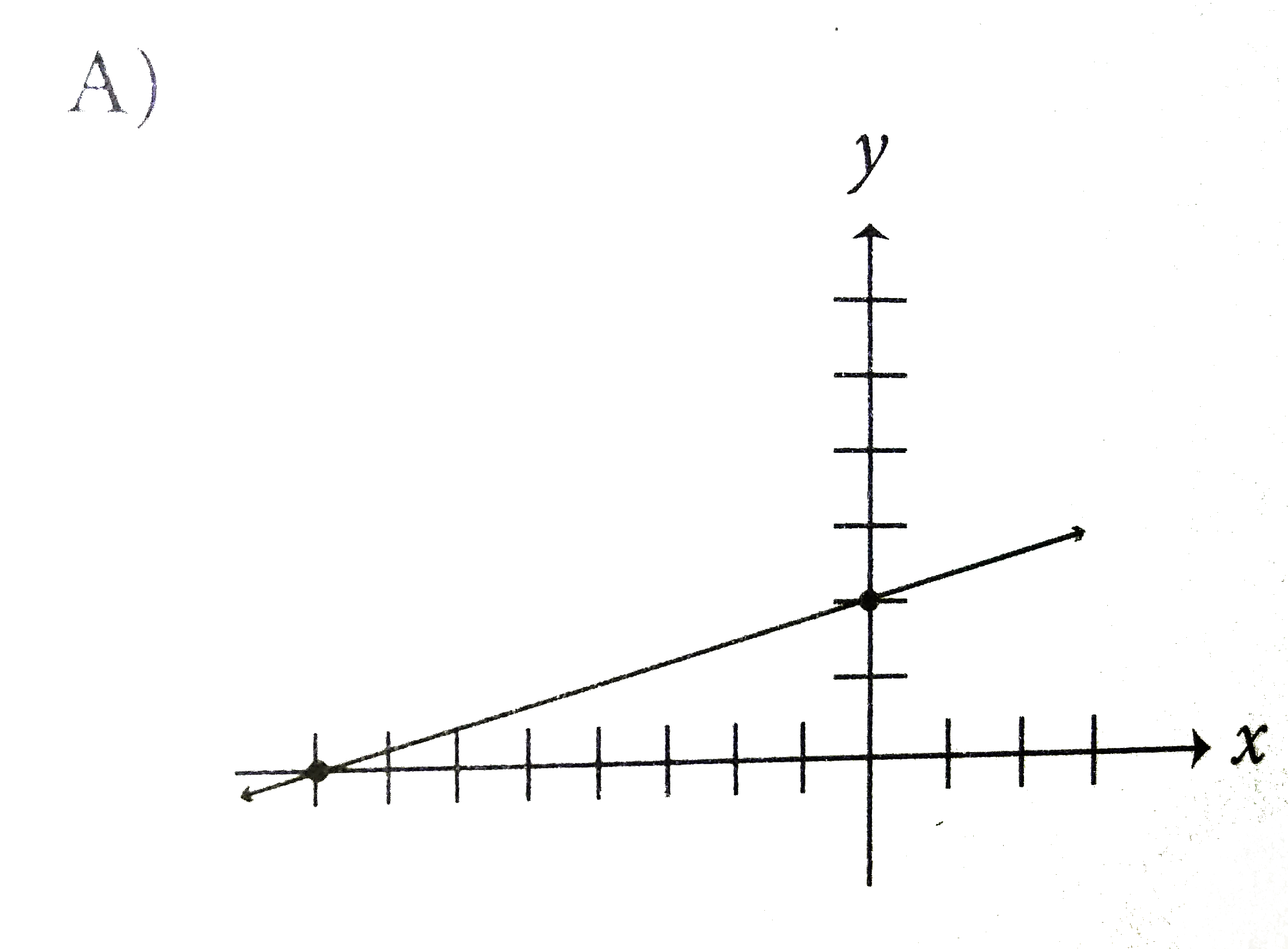 B
B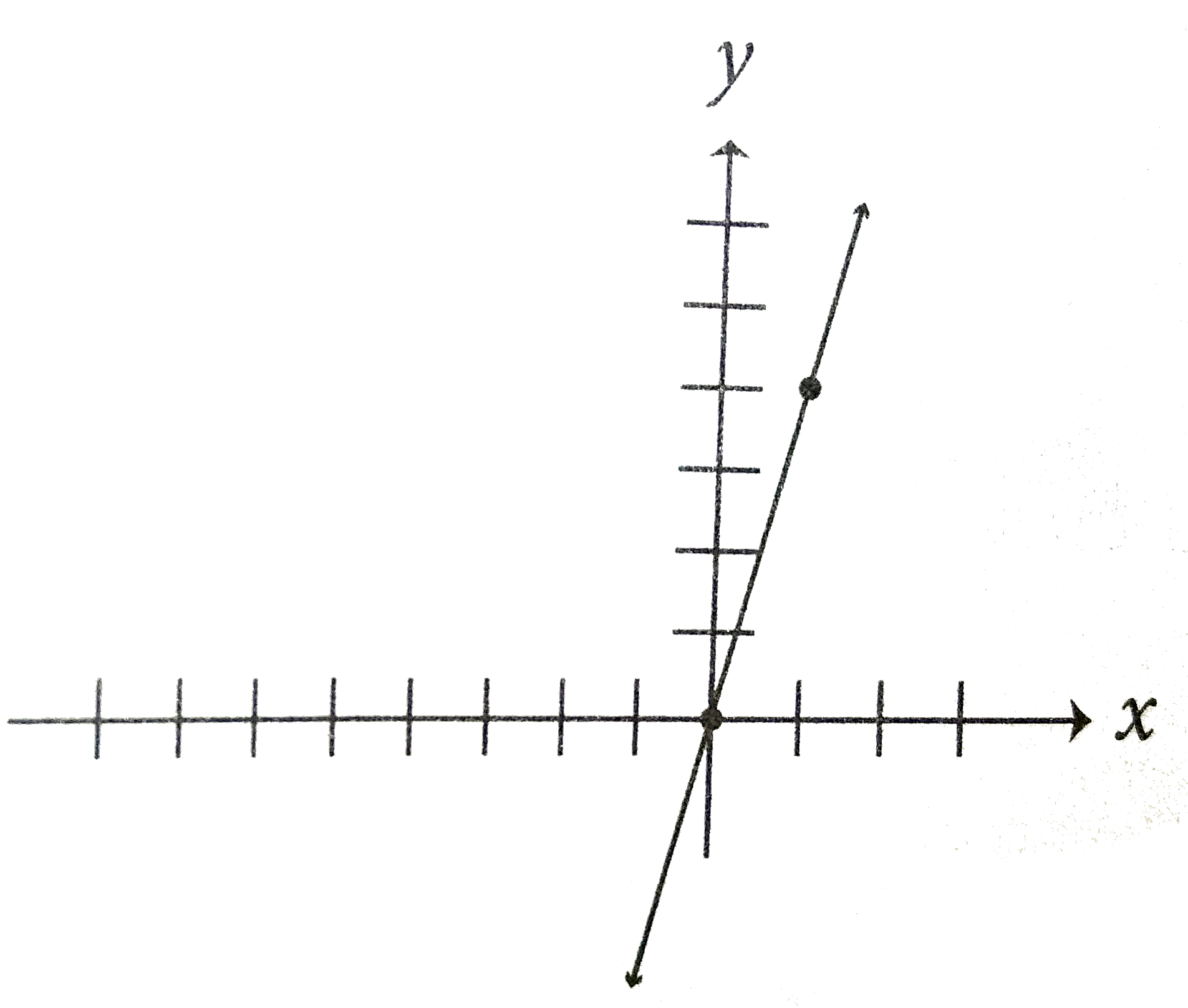 C
C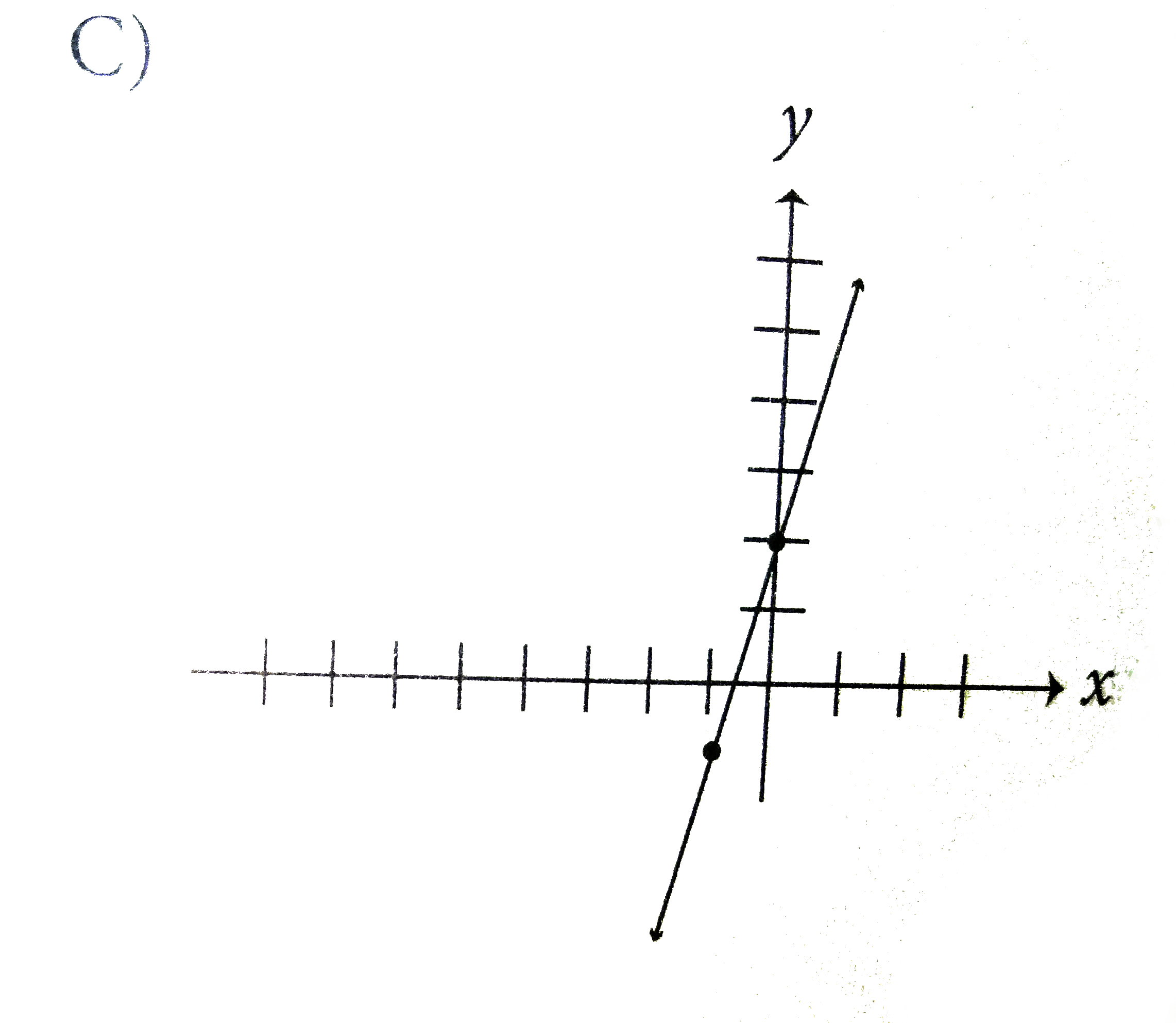 D
D
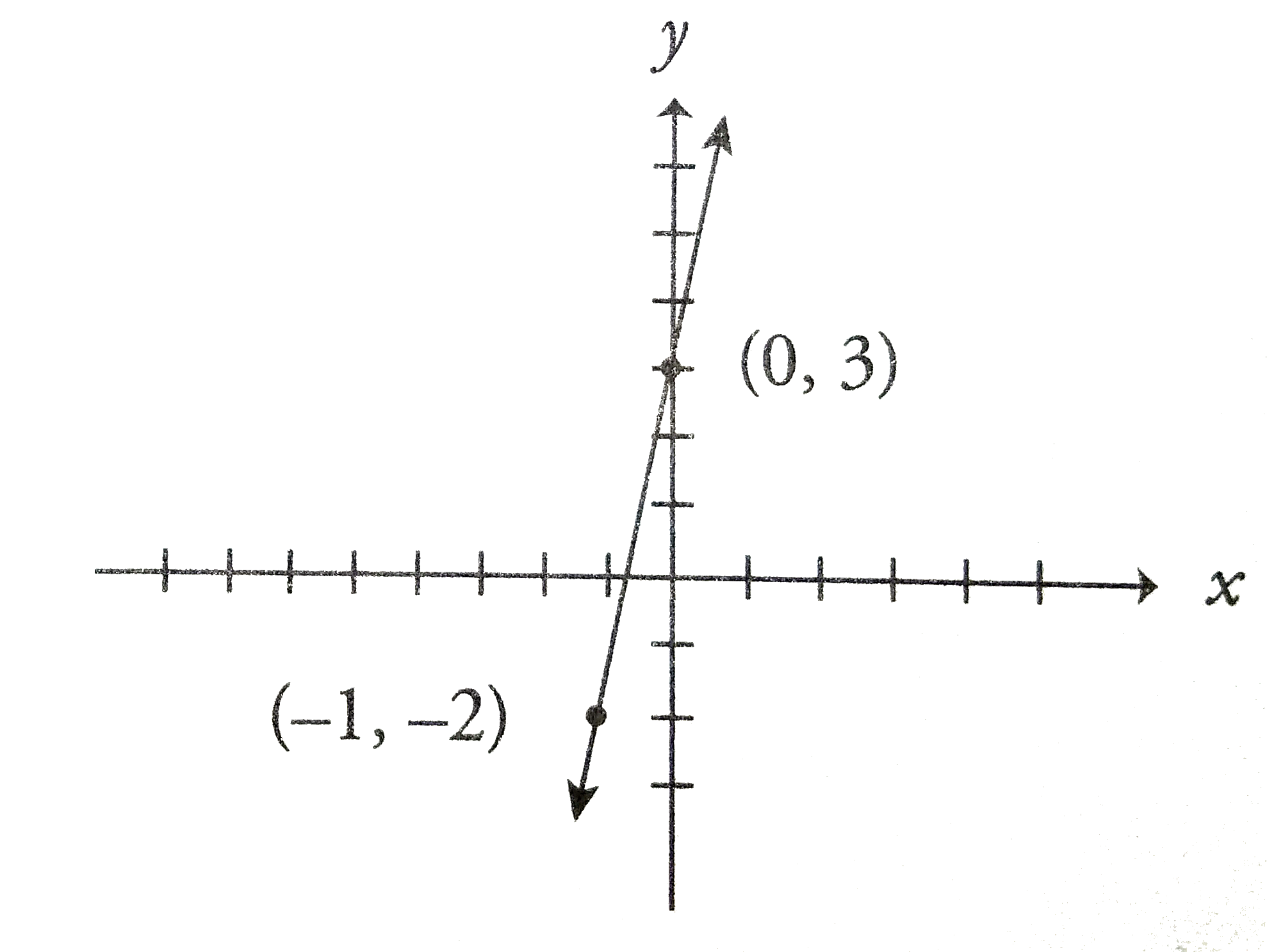
If the graph above is that of f(x), which of the following could be f(x)?Af(x)=15x+15Bf(x)=15x+3Cf(x)=3x+5Df(x)=5x+3If f(-x) = −f(x) for all x and if the point (-2,3) is on the graph of f , which of the following points must also be on the graph of f ?
A(-3,2)B(2,-3)C(-2,3)D(-2,-3)
The graph of y=|f(x)| is as shown in the following figure Fig Graph of y=f(x) may be a, b, c d is fig
View SolutionMatch the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.

View Solutionf(x)=2x+1
The function f is defined by the equation above which of the following is the graph of y=−f(x) in the xy-plane?
View Solution
If the accomanying figure above shows the graph of function f, which of the following could represent the graph of y=f(x+1)?
View Solutionf (x) = (x + 3)(x − k)
T he function f is defined above. If k is a positive integer, which of the following could represent the graph of y = f (x) in the xy-plane?
View Solution