If 22020+2021 is divided by 9, then the remainder obtained is
0
1
3
7
The correct Answer is:C
To find the remainder when 22020+2021 is divided by 9, we can follow these steps:
Step 1: Find 22020mod9
To find 22020mod9, we can use Fermat's Little Theorem, which states that if p is a prime and a is an integer not divisible by p, then ap−1≡1modp.
Here, p=9 is not prime, but we can find the powers of 2 modulo 9 directly:
- 21≡2mod9
- 22≡4mod9
- 23≡8mod9
- 24≡7mod9
- 25≡5mod9
- 26≡1mod9
Notice that 26≡1mod9, which means the powers of 2 repeat every 6 terms.
Step 2: Reduce the exponent modulo 6
Now, we need to reduce 2020 modulo 6:
2020÷6=336remainder 4
So, 2020≡4mod6.
Step 3: Calculate 22020mod9
Using the result from Step 2:
22020≡24mod9
From our earlier calculations:
24≡7mod9
Step 4: Add 2021 and find the result modulo 9
Now we calculate 22020+2021mod9:
First, find 2021mod9:
2021÷9=224remainder 5
So, 2021≡5mod9.
Now, combine the results:
22020+2021≡7+5mod9
7+5=12
Now, find 12mod9:
12÷9=1remainder 3
Final Answer
Thus, the remainder when 22020+2021 is divided by 9 is:
3
- 22≡4mod9
- 23≡8mod9
- 24≡7mod9
- 25≡5mod9
- 26≡1mod9
Topper's Solved these Questions
Similar Questions
Knowledge Check
When 221 is divided by 9, the remainder obtained is ?
Aa) 1Bb) 2Cc) 8Dd) 6When
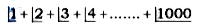 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7When
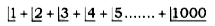 is divided by 10, the remaindeer obtained is ? A3B1C2D9
is divided by 10, the remaindeer obtained is ? A3B1C2D9
When
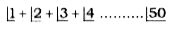 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?
View SolutionWhen 1177 is divided by 7, the remainder obtained is ?
View SolutionWhen 740 is divided by 400, the remainder obtained is ?
View SolutionWhen 4177 is divided by 17, the remainder obtained is ?
View SolutionWhen (3232)32 is divided by 9, the remainder obtained is ?
View Solution

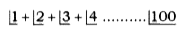 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?