When 740 is divided by 400, the remainder obtained is ?
1
6
2
3
The correct Answer is:a
To find the remainder when 740 is divided by 400, we can use the properties of modular arithmetic and the Chinese Remainder Theorem.
Step 1: Factor 400
First, we factor 400 into its prime factors:
400=16×25=24×52
Step 2: Calculate 740mod16
Now, we will calculate 740mod16:
71≡7mod16
72≡49≡1mod16
Since 72≡1mod16, we can use this to simplify 740:
740=(72)20≡120≡1mod16
Step 3: Calculate 740mod25
Next, we calculate 740mod25:
Using Euler's theorem, we first find ϕ(25):
ϕ(25)=25(1−15)=25×45=20
According to Euler's theorem:
720≡1mod25
Thus,
740=(720)2≡12≡1mod25
Step 4: Combine results using the Chinese Remainder Theorem
Now we have:
740≡1mod16
740≡1mod25
Since both congruences yield the same result, we can conclude:
740≡1mod400
Final Result
Thus, the remainder when 740 is divided by 400 is:
1
First, we factor 400 into its prime factors:
400=16×25=24×52
Now, we will calculate 740mod16:
71≡7mod16
72≡49≡1mod16
Since 72≡1mod16, we can use this to simplify 740:
740=(72)20≡120≡1mod16
Next, we calculate 740mod25:
Using Euler's theorem, we first find ϕ(25):
ϕ(25)=25(1−15)=25×45=20
According to Euler's theorem:
720≡1mod25
Thus,
740=(720)2≡12≡1mod25
Now we have:
740≡1mod16
740≡1mod25
Since both congruences yield the same result, we can conclude:
740≡1mod400
Thus, the remainder when 740 is divided by 400 is:
1
Topper's Solved these Questions
Similar Questions
Knowledge Check
When 52450 is divided by 126, the remainder obtained is ?
A5B25C125D1When
 is divided by 10, the remaindeer obtained is ? A3B1C2D9
is divided by 10, the remaindeer obtained is ? A3B1C2D9When
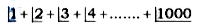 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7
When
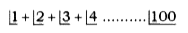 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?
View SolutionWhen 4177 is divided by 17, the remainder obtained is ?
View SolutionWhen 757575 is divided by 37, the remainder obtained is?
View SolutionWhen 1177 is divided by 7, the remainder obtained is ?
View SolutionWhen
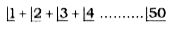 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?
View Solution
