If 5353−333 is divided by 10, then the remainder obtained is
The correct Answer is:6
To find the remainder when 5353−333 is divided by 10, we can use modular arithmetic. Here’s a step-by-step solution:
Step 1: Calculate 5353mod10
First, we simplify 53mod10:
53≡3mod10
Thus, we can rewrite 5353 as:
5353≡353mod10
Step 2: Find the pattern in 3nmod10
Next, we need to find 353mod10. We can observe the powers of 3 modulo 10:
- 31≡3mod10
- 32≡9mod10
- 33≡27≡7mod10
- 34≡81≡1mod10
The pattern repeats every 4 terms: 3,9,7,1.
Step 3: Determine the exponent modulo 4
To find 353mod10, we need to determine 53mod4:
53÷4=13(remainder 1)
Thus, 53≡1mod4.
Step 4: Use the pattern to find 353mod10
From the pattern, since 53≡1mod4:
353≡31≡3mod10
Step 5: Calculate 333mod10
Now, we simplify 33mod10:
33≡3mod10
Thus, we have:
333≡33mod10
From our previous calculations:
33≡7mod10
Step 6: Combine results
Now we can substitute back into our original expression:
5353−333≡3−7mod10
Calculating this gives:
3−7≡−4mod10
To convert −4 into a positive remainder, we add 10:
−4+10=6
Final Answer
Thus, the remainder when 5353−333 is divided by 10 is:
6
53≡3mod10
Thus, we can rewrite 5353 as:
5353≡353mod10
- 31≡3mod10
- 32≡9mod10
- 33≡27≡7mod10
- 34≡81≡1mod10
53÷4=13(remainder 1)
Thus, 53≡1mod4.
353≡31≡3mod10
33≡3mod10
Thus, we have:
333≡33mod10
From our previous calculations:
33≡7mod10
5353−333≡3−7mod10
Calculating this gives:
3−7≡−4mod10
To convert −4 into a positive remainder, we add 10:
−4+10=6
6
Topper's Solved these Questions
Similar Questions
Knowledge Check
When
 is divided by 10, the remaindeer obtained is ? A3B1C2D9
is divided by 10, the remaindeer obtained is ? A3B1C2D9When
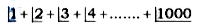 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7When
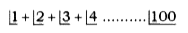 , is divided by 5, the remainder obtained is ?A0B1C2D3
, is divided by 5, the remainder obtained is ?A0B1C2D3
When 355 is divided by 82, the remainder obtained is ?
View SolutionWhen 740 is divided by 400, the remainder obtained is ?
View SolutionWhen 4177 is divided by 17, the remainder obtained is ?
View SolutionWhen (35)37 is divided by 9 the remainder obtained is ?
View SolutionWhen 242 is divided by 33, the remainder obtained is ?
View Solution

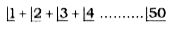 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?