If a circle of radius b units with centre at (0,b) touches the line y=x−√2 , then what is the value of b ?
A
2+√2
B
2−√2
C
2√2
D
√2
Video Solution
Text Solution
The correct Answer is:A
Distance from the centre to the point of line which touches circle is OM= radius
y=x−√2 orx−y−√2=0
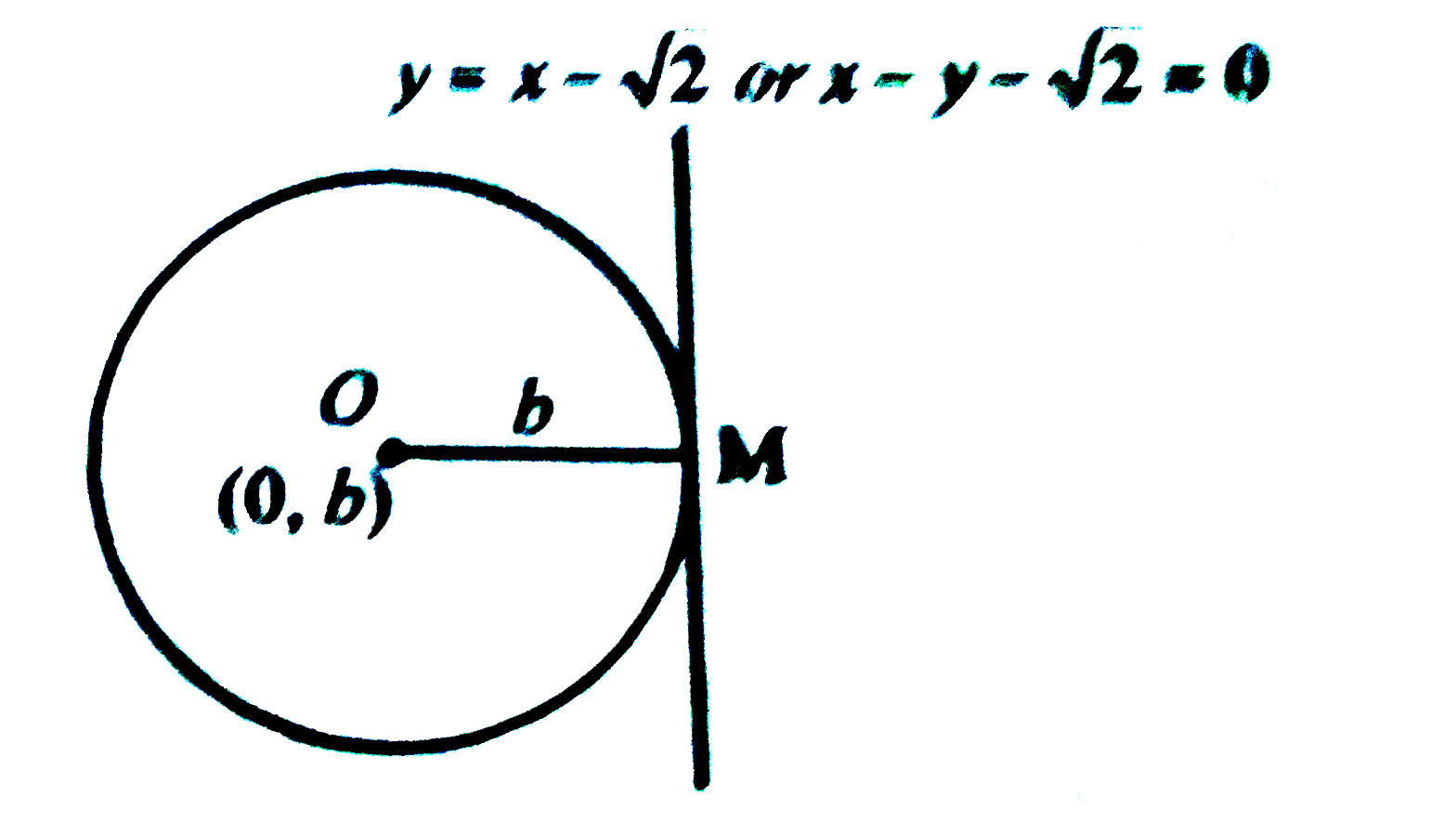
r=|Ax0+By0+C|√A2+B2
∵x0=0
& Y0=b
b=∣∣1(0)+(−1)(b)−√2∣∣√(1)2+(−1)2
b=b+√2√2
(√2−1)b=√2
⇒b=2+√2
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a circle of radius b units with centre at (0,b) touches the line y=x−√2 , then what is the value of b ?
A2+√2B2−√2C2√2D√2If a circle of radius 3 units is touching the lines √3y2−4xy+√3x2=0 in the first quadrant then length of chord of contact to this circle is :
A√3+12B√3+1√2C3(√3+1√2)D3(√3+1)2The equation of the circle of radius 2√2 whose centre lies on the line x−y=0 and which touches the line x+y=4, and whose centre is coordinate satisfy x+y>4, is
Ax2+y2−8x−8y+24=0Bx2+y2=8Cx2+y2−8x+8y−24=0Dnone of these
If (α,α) is a point on the circle whose centre is on the x-axis and which touches the line x+y=0 at (2,−2), then the greatest value of 'α' is
View SolutionIf a circle drawn with radius 1 unit and whose centre is the focus of the parabola y2=4x touches the parabola at
View SolutionThe centre of a circle (1,1) and its radius is 5 units. If the centre is shifted along the line y−x=0 through a dis-tance √2 units. Find the equation(s) of the circle(s) in the new position.
View Solutionchord of contact of the tangents drawn from a point on the circle x2+y2=81 to the circle x2+y2=b2 touches the circle x2+y2=16, then the value of b is
View SolutionA circle touches both the coordinate axes and the line x−y=√2a,a>0, the coordinates of the centre of the circle cannot be
View Solution
