If a diagonal of a parallelogram bisects one of the angles of the parallelogram, prove that it also bisects the angle opposite it, and that the two diagonals are perpendicular to each other.
Also, prove that it is a rhombus.
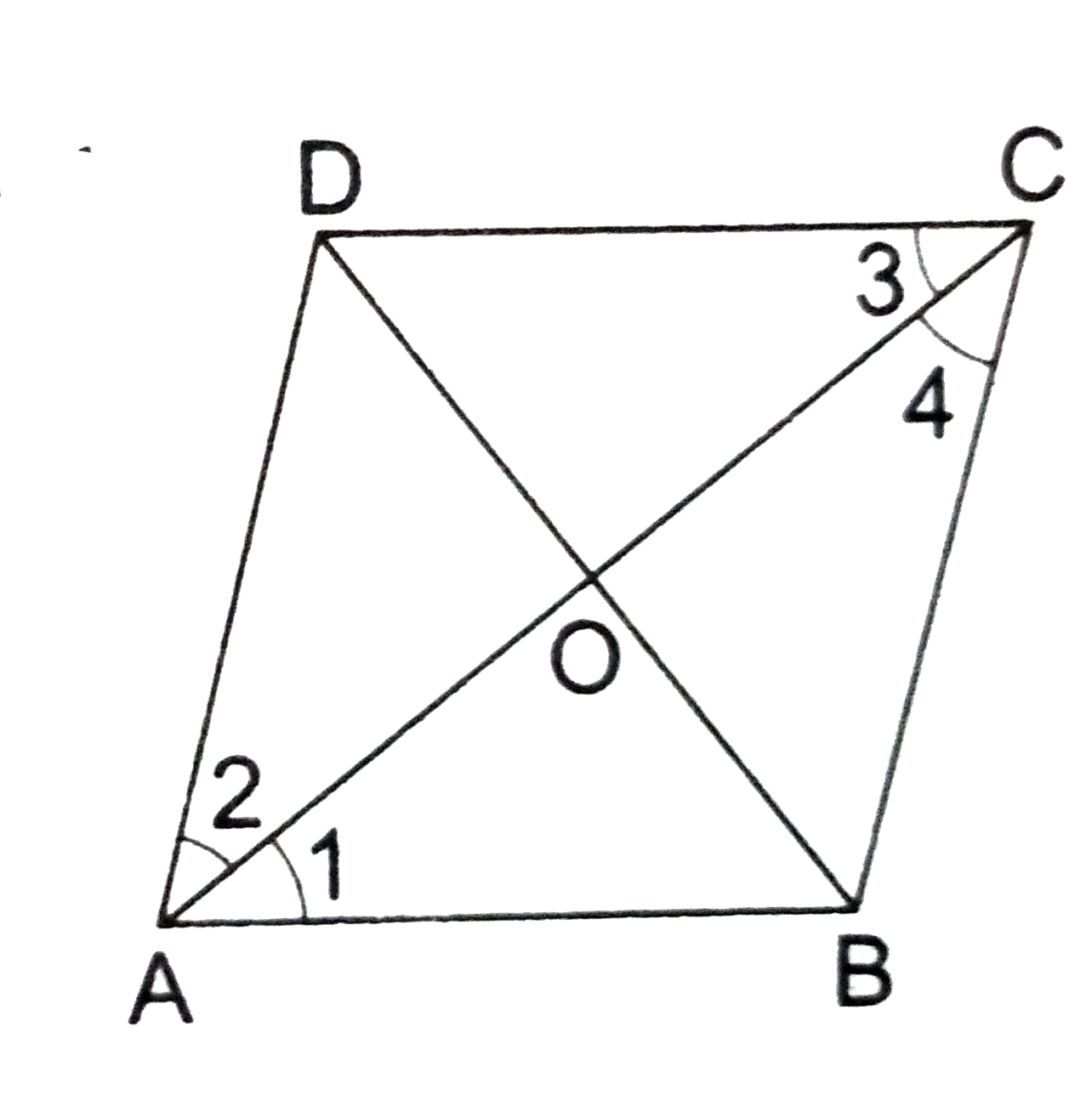
Given A||gm ABCD whose diagonals AC and BD intersect at O. Also, AC bisects ∠A, i.e., ∠1=∠2.
TO PROVE (i) AC bisects ∠C, i.e., ∠3=∠4.
(ii) AC⊥BD.
(iii) ABCD is a rhombus.
PROOF In ||gm ABCD , we have
AB||DC and CA cuts them
∴∠1=∠3 (alt. interior ∠)
and AD||BC and CA cuts them
∴∠2=∠4 (alt. interior ∠).
Now, ∠1=∠2⇒∠3=∠4.
This shows that AC bisects ∠C also.
Now, ∠A=∠C (opp. ∠of a ||gm).
⇒12∠A=12∠C⇒∠2=∠3⇒AD=DC.
But, AB=DCandAD=BC.
∴AB=BC=DC=AD.
So, ABCD is a rhombus.
But, the diagonals of a rhombus bisect each other at right angles.
∴AC⊥BD.
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
In a diagonal of a parallelogram bisects one of the angles of the parallelogram; it also bisects the second angle.
View SolutionIf diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle.
View SolutionThe diagonals of a parallelogram bisect each other.
View SolutionThe diagonals of a parallelogram bisect each other.
View SolutionThe diagonals of a parallelogram bisect each other.
View SolutionIf diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle. Also, prove that it is a rhombus.
View Solutionif diagonals of a parallelogram bisect each other,prove that its a rhombus
View Solutionif diagonals of a parallelogram bisect each other,prove that its a rhombus
View SolutionThe diagonals of parallelogram bisect each other ( True/ False)
View SolutionProve that the diagonals of a parallelogram bisect each other.
View Solution
