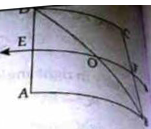
Let ABCD be a trapezium in which AB||DC and let E be the midpoint of AD. Let F be a point on BC such that EF||AB. Prove that
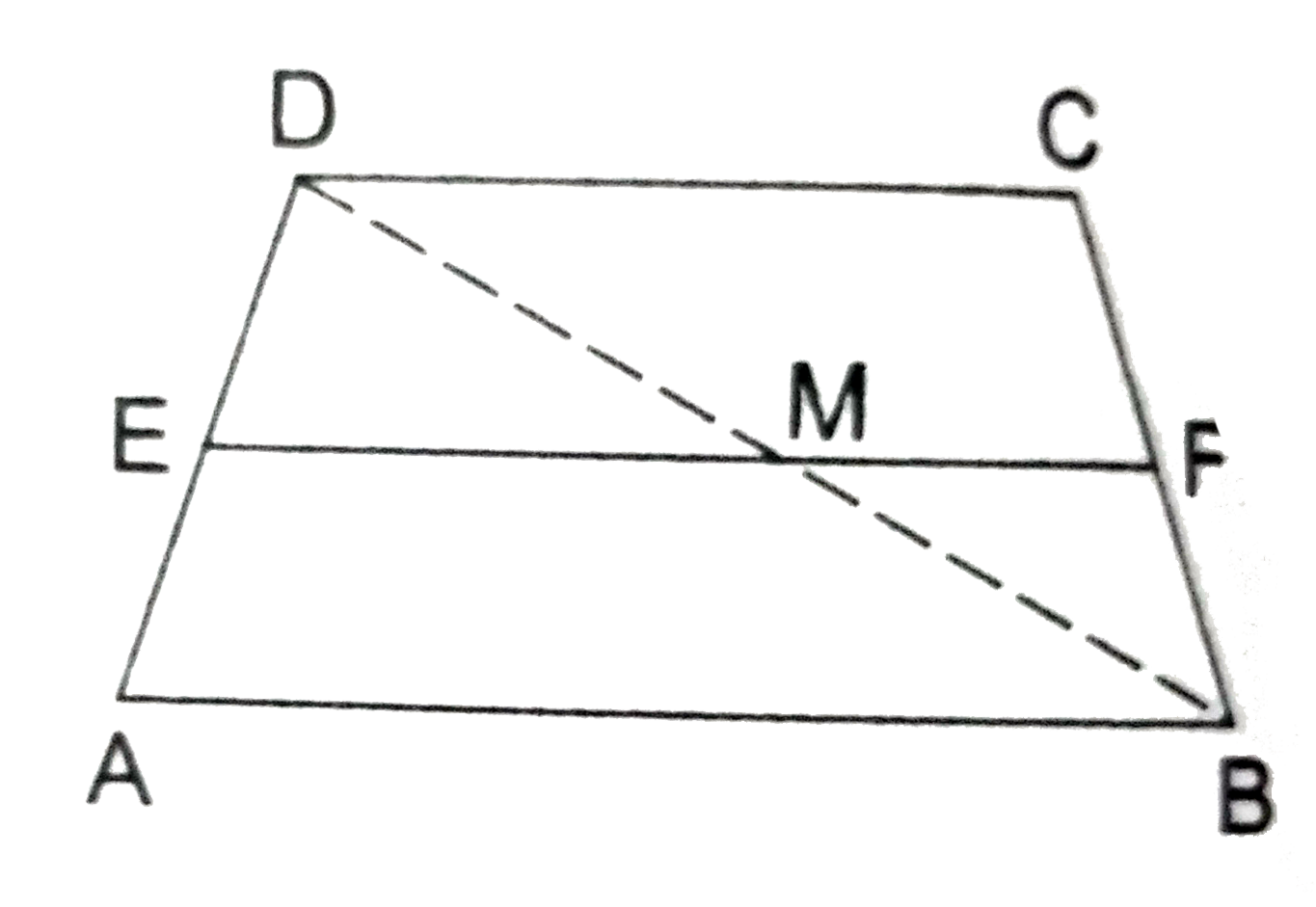
(i) F is the midpoint of BC, (ii) EF=12(AB+DC).
Join BD, cutting EF at M.
Now, in △DAB, E is the midpoint of AD and EM||AB.
∴ M is the midpoint of BD.
∴EM=12AB …(i)
Again, in △ BDC, M is the midpoint of BD and MF||DC.
∴ F is the midpoint of BC.
∴MF=12DC. ...(ii)
∴EF=EM+MF=12(AB+DC) [from (i) and (ii) ].
Hence, F is the midpoint of BC and EF=12(AB+DC).
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A10videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B27videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
ABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:
 View Solution
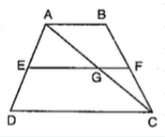
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Let ABCD be a trapezium in which AB||DC and E be the mid-point of AD. If F be a point on BC such that EF||AB. Then EF, where F is the mid-point of BC, is equal to
 AAB + DCB12(AB+DC)C13(AB+DC)DNone of these
AAB + DCB12(AB+DC)C13(AB+DC)DNone of these - Question 2 - Select One
ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2 - Question 3 - Select One
ABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
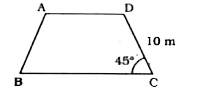 A10√2mB4√2mC5√2mD6√2m
A10√2mB4√2mC5√2mD6√2m
In the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionIn the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
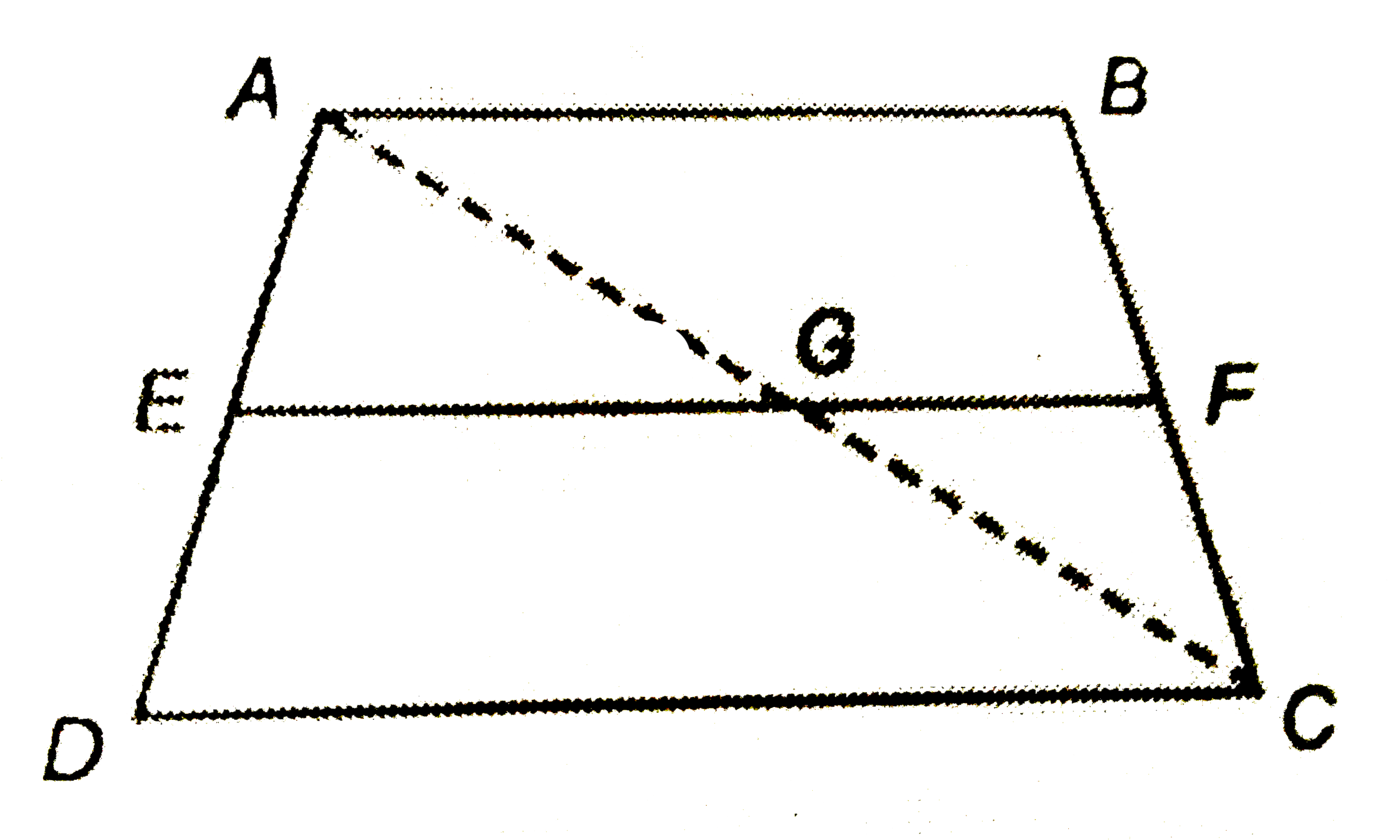 View Solution
View SolutionABCD is a trapezium with AB || DC. E is midpoint of side AD. From point E a line is drawn parallel to AB that intersects BC at F. Show that F is midpoint of BC.
 View Solution
View SolutionE and F are respectively the midpoints of the non-parallel sides AD and BC of a trapezium ABCD. Prove that
(i) EF∣∣AB,
(ii) EF=12(AB+CD).View SolutionLet ABC be a triangle such that AB=BC. Let F be midpoint of AB and X be a poin on BC such that FX is perpendicular to AB. If BX =3XC then the ratio BC/AC equals
View Solution

