In the adjoining figure, points M and N divide the side AB of △ABC into three equal parts. Line segments MP and NQ are both parallel to BC and meet AC in P and Q respectively. Prove that P and Q divide AC into three equal parts.
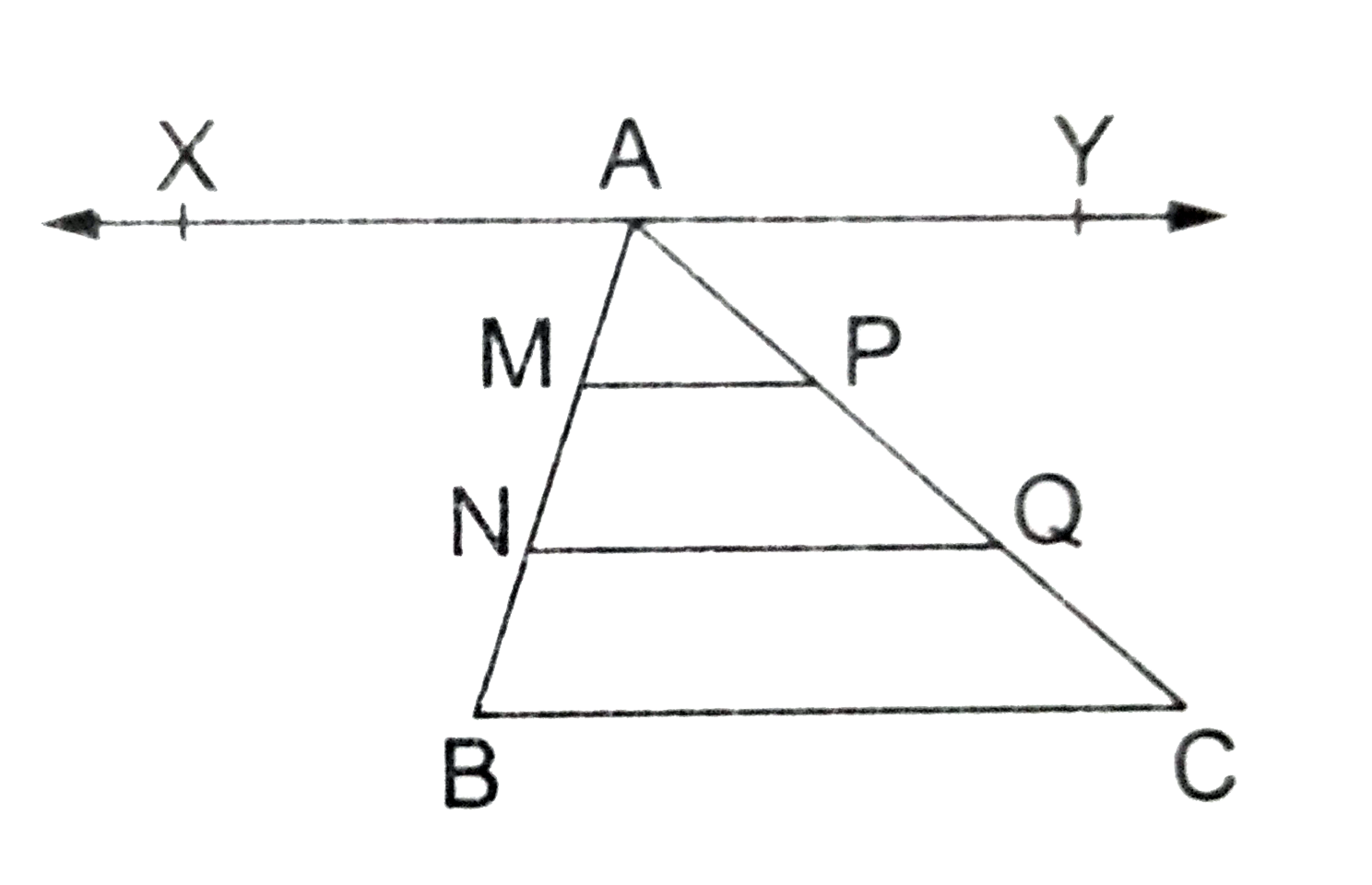
Through A, draw XAY||BC.
Now, XY||MP||NQ are cut by the transversal AB at A, M, N respectively such that AM = MN.
Also, XY||MP||NQ are cut by the transversal AC at A, P, Q respectively.
∴AP=PQ …(i) (by intercept theorem).
Again, MP||NQ||BC are cut by the transversal AC at P, Q, C respectively.
∴PQ=QC ...(ii) (by intercept theorem).
Thus, from (i) and (ii), we get AP=PQ=QC.
Hence, P and Q divide AC into three equal parts.
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
M and N divide the side AB of a triangle ABC into three equal parts . Through M and N, lines are drawn parallel to BC and intersecting AC at points P and Q respectively. Prove that P and Q divide AC into three equal parts.
View SolutionDraw a line segment of length 8 cm . Divide it into three equal parts .
View Solution
Knowledge Check
In the adjoining figure, P and Q are two points on equal sides AB and AC of a isosceles triangle ABC such that AP = AQ, then
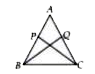 ABQ = CPB∠ABQ=∠ACPC∠BAQ=∠CPADboth (a) and (b)
ABQ = CPB∠ABQ=∠ACPC∠BAQ=∠CPADboth (a) and (b)
The points M and N divide the line seqment AB of ΔABC in three equal parts. If MP||NQ||BC and points P and Q lie on line AC, then prove that P and Q trisect the line AC.
View SolutionEach side of triangle ABC is divided into three equal parts. Find the ratio of the are of hexagon PQRSTU to the area of the triangle ABC.
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.

(iii) Find the ratio in which Q divides AC.
View SolutionEach side of triangle ABC is divided into three equal parts. Find the ratio of the area of hexagon PQRSTU to the area of the triangle ABC.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

View SolutionIn the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
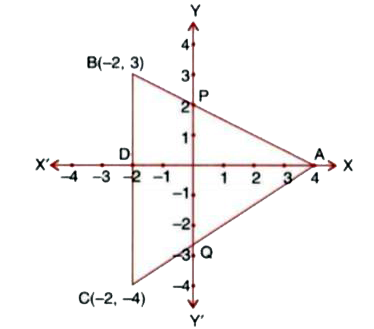
Find the ratio in which divides AC.
View Solution
