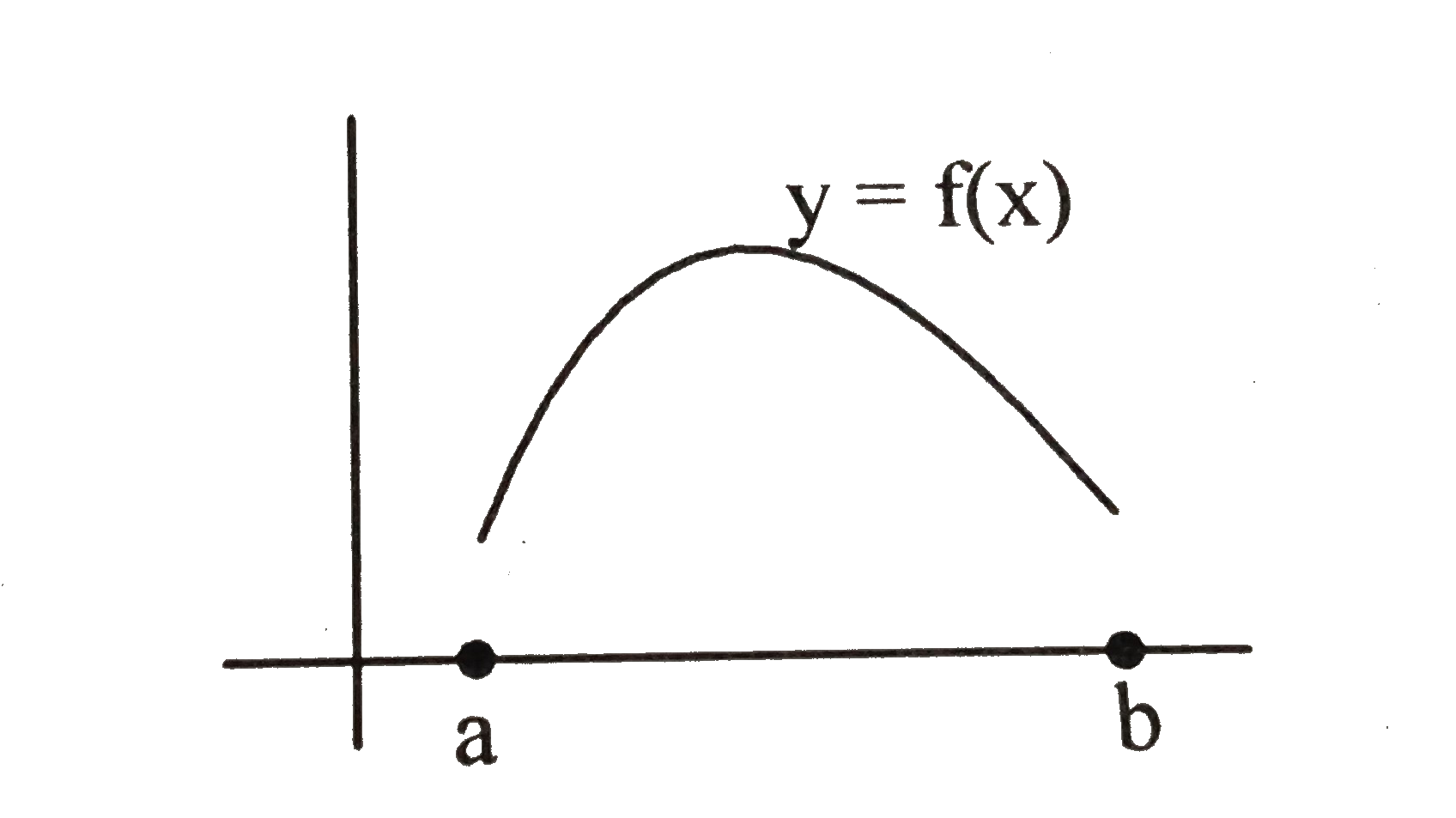
If a function (continuos and twice differentiable) is always concave upward in an interval, then its graph lies always below the segment joining extremities of the graph in that interval and vice-versa.
Let f:R+→R+ is such that f(x)≥0∀x∈[a,b]. Then value of ∫baf(x)dx cannot exceed:Solution in Punjabi
(f(a)+f(b))(b−a)3
(f(b)−f(a))(b−a)2
(f(b)+f(a))(b−a)2
None of the above
Step by step video & image solution for If a function (continuos and twice differentiable) is always concave upward in an interval, then its graph lies always below the segment joining extremities of the graph in that interval and vice-versa. Let f:R^(+)toR^(+) is such that f"(x)ge0 AAx in [a,b]. Then value of int_(a)^(b)f(x) dx cannot exceed: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise For Session 17videos
MONOTONICITY MAXIMA AND MINIMA
- BOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise For Session 24videos
MONOTONICITY MAXIMA AND MINIMA
- BOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)31videos
MONOTONICITY MAXIMA AND MINIMA
- BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)49videos
MATRICES
- BOOK - ARIHANT MATHSCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)2videos
PAIR OF STRAIGHT LINES
Similar Questions
Evaluate n!(n−r)! , when n = 7 , r = 4
11:12View SolutionDetermine all the critical points for the function f(x)=6x5+33x4−30x3+100
04:37View SolutionThe least value of α∈R for which 4ax2+1x≥1, for all x>0, is
04:32View SolutionLet A=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦andA−1=[16(A2+cA+dI)] Then value of candd are (a) (−6,−11) (b) (6,11) (c) (−6,11) (d) (6,−11)
View SolutionIf the pair of lines ax2+2(a+b)xy+by2=0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
01:21View SolutionThe graph of the derivative f of a continuous function fis~ shown with f(0)=0, then for f(x) find (i) Intervals of monotonicity (ii) Intervals of concavity
02:08View SolutionLet f:R rarr R be a differentiable function such that f(a)=0=f(b) and f'(a)f'(b)>0 for some a
03:57View SolutionThe following figure shows the graphs of a differentiable fucntion y=f(x) on the interval [a,b] (not contaning 0).
Let g(x)=f(x)/x which of the following is a possible graph of y=g(x) ?03:25View SolutionIf f(x) is double differentiable function such that |f"(x)|le5 for each x in the interval [0,4] and f takes its largest value at an interior point of this interval , then value of |f'(0)|+|f,'(4)| cannot be -
View SolutionLet f:R→R be a function defined by f(x)=|x|3+|x|1+x2, then the graph of f(x) lies in the
View SolutionLet f(x) be a differentiable function in the interval (0, 2) then the value of ∫20f(x)dx
02:20View SolutionLet f:[a,b]→R be such that f is differentiable in (a,b), f is continuous at x=a and x=b and moreover f(a)=0f(b). Then
04:28View SolutionLet f(x) be a differentiable function in the interval (0,2) then the value of ∫20f(x) is
06:37View SolutionLet the function, f:[−7,0]→R be continuous on [−7,0] and differentiable on (−7,0). If f(−7)=−3 and f'(x)≤2, for all x∈(−7,0), then for all such functions f,f(−1)+f(0) lies in the interval :
03:04View SolutionProceeding from geometric reasoning, prove that :
(a) if the function f(x) increases and has a concave graph in the interval [a,b], then
(b,a)f(a)<∫baf(x)dx<(b−a)f(a)+f(b)2
(b) if the function f(x) increases and has a convex graph in the interval [a,b], then
(b−a)f(a)+f(b)2<∫baf(x)dx<(b−a)f(b)02:52View SolutionLet f(x) be a differentiable function in the interval (0,2) , then the value of ∫20f(x)dx is :
02:03View Solution

