If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral, so formed is cyclic.
Given ΔABC is an isosceles triangle such that AB=AC and also DE∣∣BC.
To prove Quadrilateral BCDE is a cyclic quadrilateral.
Construction Draw a circle passes through the points B, C, D and E.
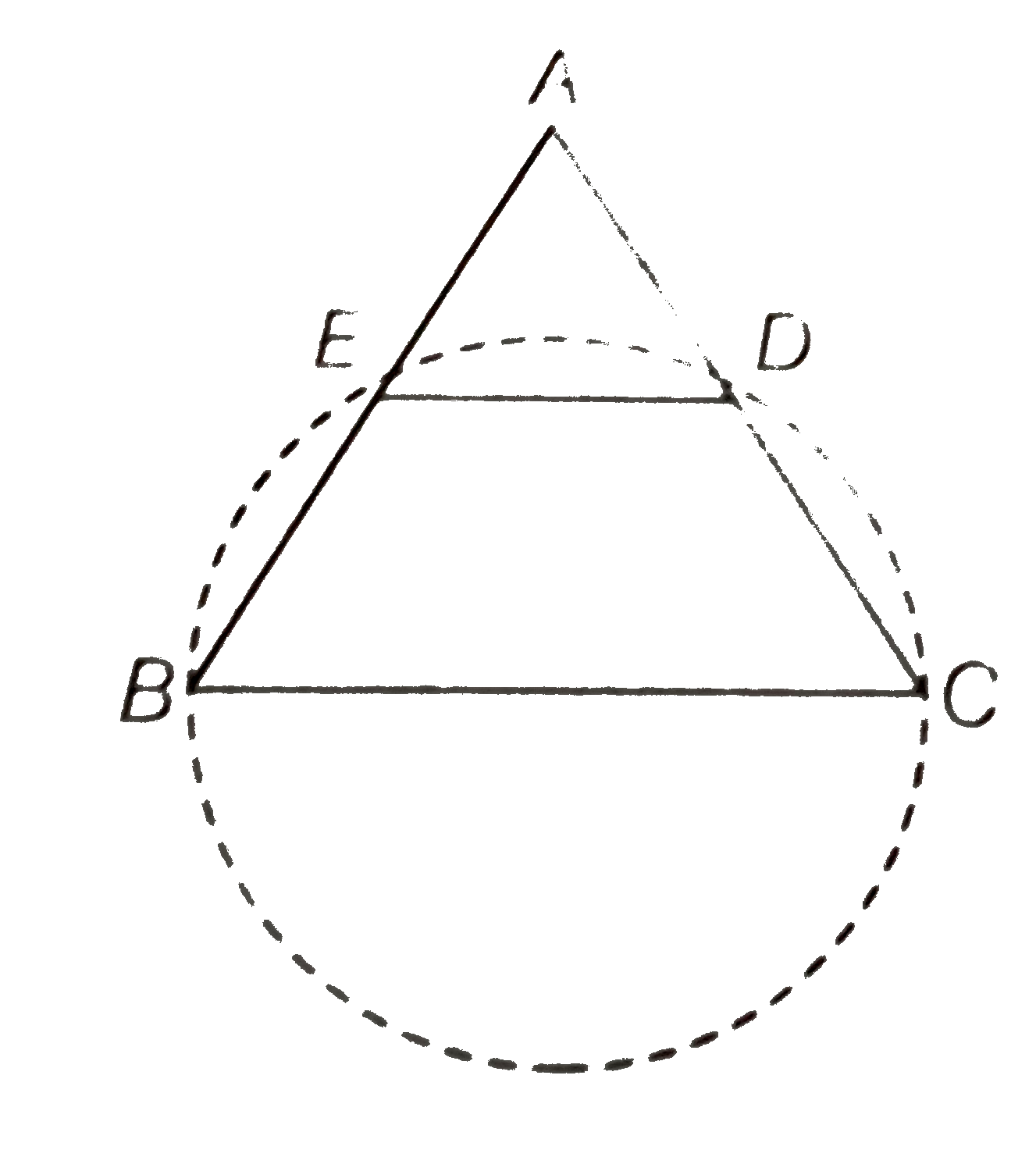
Proof In ΔABC,AB=AC [equal sides of an isosceles triangle]
⇒∠ACB=∠ABC...(i)
[angle opposite to the equal sides are equal]
Since, DE∣∣BC
⇒∠ADE=∠ACB [corresponding angles]...(ii)
On adding both sides by ∠EDC in Eq. (ii), we get
∠ADE+∠EDC=∠ACB+∠EDC
⇒180∘=∠ACB+∠EDC
[∠ADEand∠EDC form linear pair aniom]
⇒∠EDC+∠ABC=180∘ [form Eq. (i)]
Hence, BCDE is a cyclic quadrilateral, because sum of the opposite angles is 180∘.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.42videos
CIRCLES
- BOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles34videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
Similar Questions
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
View SolutionProve that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View Solution
Knowledge Check
- Question 1 - Select One
The base of an isosceles triangle is 6 cm and each of its equal sides is 5 cm. The height of the triangle is
A8 cmB√30 cmC4 cmD√11 cm - Question 2 - Select One
The base of an isosceles triangle is 8 cm long and each of its equal sides measures 6 cm. The area of the triangle is
A16√5cm2B8√5cm2C16√3cm2D8√3cm2 - Question 3 - Select One
The base of an isosceles triangle is 16 cm. If both the equal sides be 17 cm each, find the area of the triangle.
A90 cm2B100 cm2C120 cm2D110 cm2
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 DE||BC and BD = CE. Prove that ΔABC is an isosceles triangle.
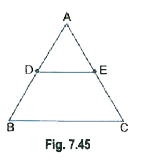 View Solution
View SolutionThe base of an isosceles triangle is 300 units and each of its equal sides is 170 units. Then the area of the triangle is
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
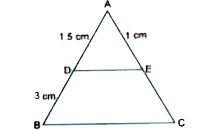
View SolutionIf a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE∣∣BC.
 View Solution
View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
View Solution

