If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
To prove that the exterior angles formed by extending the base of an isosceles triangle are equal to each other, we can follow these steps:
1. Identify the Triangle: Let triangle ABC be an isosceles triangle where AB = AC.
2. Label the Angles: Since AB = AC, by the properties of isosceles triangles, the angles opposite these sides are equal. Therefore, we have:
∠B=∠C
3. Extend the Base: Extend the base BC on both sides to points D and E, creating the exterior angles ∠ACD and ∠ABE.
4. Identify Linear Pairs: Since angles ACD and ABC are on a straight line, they form a linear pair. Thus:
∠ACD+∠ABC=180∘
This implies:
∠ACD=180∘−∠ABC
5. Substitute Equal Angles: We know that ∠ABC = ∠B (since they are the same angle). Therefore, we can write:
∠ACD=180∘−∠B
6. Similarly for the Other Angle: Now, looking at the angles ABE and ABC, we also have:
∠ABE+∠ABC=180∘
Thus:
∠ABE=180∘−∠ABC
Substituting again, we find:
∠ABE=180∘−∠B
7. Equate the Two Angles: Now we have:
∠ACD=180∘−∠B
∠ABE=180∘−∠B
Since both angles are equal to 180∘−∠B, we conclude that:
∠ACD=∠ABE
8. Conclusion: Hence, we have proved that the exterior angles formed by extending the base of the isosceles triangle are equal to each other.
∠B=∠C
∠ACD+∠ABC=180∘
This implies:
∠ACD=180∘−∠ABC
∠ACD=180∘−∠B
∠ABE+∠ABC=180∘
Thus:
∠ABE=180∘−∠ABC
Substituting again, we find:
∠ABE=180∘−∠B
∠ACD=180∘−∠B
∠ABE=180∘−∠B
Since both angles are equal to 180∘−∠B, we conclude that:
∠ACD=∠ABE
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If the sides of a triangle are extended in both the sides then the sum of the exterior angles so formed in both sides is
A360∘B540∘C720∘D180∘ - Question 2 - Select One
If the sides of a triangle are produced then the sum of the exterior angles i.e,
∠DAB+∠EBC+∠FCA is equal to :
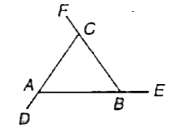 A180∘B270∘C360∘D240∘
A180∘B270∘C360∘D240∘ - Question 3 - Select One
The base of an isosceles triangle is 6 cm and each of its equal sides is 5 cm. The height of the triangle is
A8 cmB√30 cmC4 cmD√11 cm
If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral, so formed is cyclic.
View SolutionIf the bisector of the vertical angle of a triangle bisects the base, prove that the triangle is isosceles.
View SolutionTheorem 6.8 : If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
View SolutionIf the side BC of ABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A
View Solution

