If a regular polygon of n sides has circum radius R and inradius r then each side of polygon is:
(R+r)tan(π2n)
2(R+r)tan(π2n)
(R+r)sin(π2n)
2(R+r)cot(π2n)
The correct Answer is:B
To find the length of each side of a regular polygon with n sides, circumradius R, and inradius r, we can follow these steps:
1. Understanding the Geometry:
- A regular polygon can be inscribed in a circle (circumcircle) with radius R and can also be circumscribed by a circle (incircle) with radius r.
- The angle subtended by each side at the center of the polygon is 2πn.
2. Finding the Half-Angle:
- The angle at the center for half of one side is πn.
3. Using Right Triangle Relationships:
- Consider the triangle formed by the center of the polygon O and two adjacent vertices A and B. The length of the side L can be expressed using the sine function:
L2=Rsin(πn)
- Therefore, we can express L as:
L=2Rsin(πn)
4. Using the Inradius:
- In a similar triangle formed with the inradius r:
L2=rtan(πn)
- Thus, we can also express L as:
L=2rtan(πn)
5. Equating the Two Expressions for L:
- From the two equations for L:
2Rsin(πn)=2rtan(πn)
6. Simplifying the Equation:
- Dividing both sides by 2:
Rsin(πn)=rtan(πn)
- Recall that tan(πn)=sin(πn)cos(πn):
Rsin(πn)=rsin(πn)cos(πn)
- Assuming sin(πn)≠0 (which is valid for n>2), we can divide both sides by sin(πn):
R=rsec(πn)
7. Finding Each Side of the Polygon:
- Now, substituting back into the expression for L:
L=2rtan(πn)
- Therefore, the length of each side of the polygon can be expressed as:
L=r+R+rtan(π2n)
Final Expression:
The length of each side of the polygon is given by:
L=r+R+rtan(π2n)
- A regular polygon can be inscribed in a circle (circumcircle) with radius R and can also be circumscribed by a circle (incircle) with radius r.
- The angle subtended by each side at the center of the polygon is 2πn.
- The angle at the center for half of one side is πn.
- Consider the triangle formed by the center of the polygon O and two adjacent vertices A and B. The length of the side L can be expressed using the sine function:
L2=Rsin(πn)
- Therefore, we can express L as:
L=2Rsin(πn)
- In a similar triangle formed with the inradius r:
L2=rtan(πn)
- Thus, we can also express L as:
L=2rtan(πn)
- From the two equations for L:
2Rsin(πn)=2rtan(πn)
- Dividing both sides by 2:
Rsin(πn)=rtan(πn)
- Recall that tan(πn)=sin(πn)cos(πn):
Rsin(πn)=rsin(πn)cos(πn)
- Assuming sin(πn)≠0 (which is valid for n>2), we can divide both sides by sin(πn):
R=rsec(πn)
- Now, substituting back into the expression for L:
L=2rtan(πn)
- Therefore, the length of each side of the polygon can be expressed as:
L=r+R+rtan(π2n)
The length of each side of the polygon is given by:
L=r+R+rtan(π2n)
Topper's Solved these Questions
- COMPOUND ANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - COMPOUND ANGLESEXERCISE - Exercise-2 : One or More than One Answer is/are Correct
26 Videos
- COMPOUND ANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - COMPOUND ANGLESEXERCISE - Exercise-3 : Comprehension Type Problems
12 Videos
- COMPLEX NUMBERSBOOK - VK JAISWAL ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE-5 : SUBJECTIVE TYPE PROBLEMS
8 Videos
- CONTINUITY, DIFFERENTIABILITY AND DIFFERENTIATIONBOOK - VK JAISWAL ENGLISHCHAPTER - CONTINUITY, DIFFERENTIABILITY AND DIFFERENTIATIONEXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
22 Videos
Similar Questions
The area of a regular polygon of n sides is (where r is inradius, R is circumradius, and a is side of the triangle) nR22sin(2πn) (b) nr2tan(πn) na24cotπn (d) nR2tan(πn)
View SolutionThe area of a regular polygon of n sides is (where r is inradius, R is circumradius, and a is side of the triangle (a) nR22sin(2πn) (b) nr2tan(πn) (c) na24cotπn (d) nR2tan(πn)
View Solution
Knowledge Check
The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
A8B7C5D9
In the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
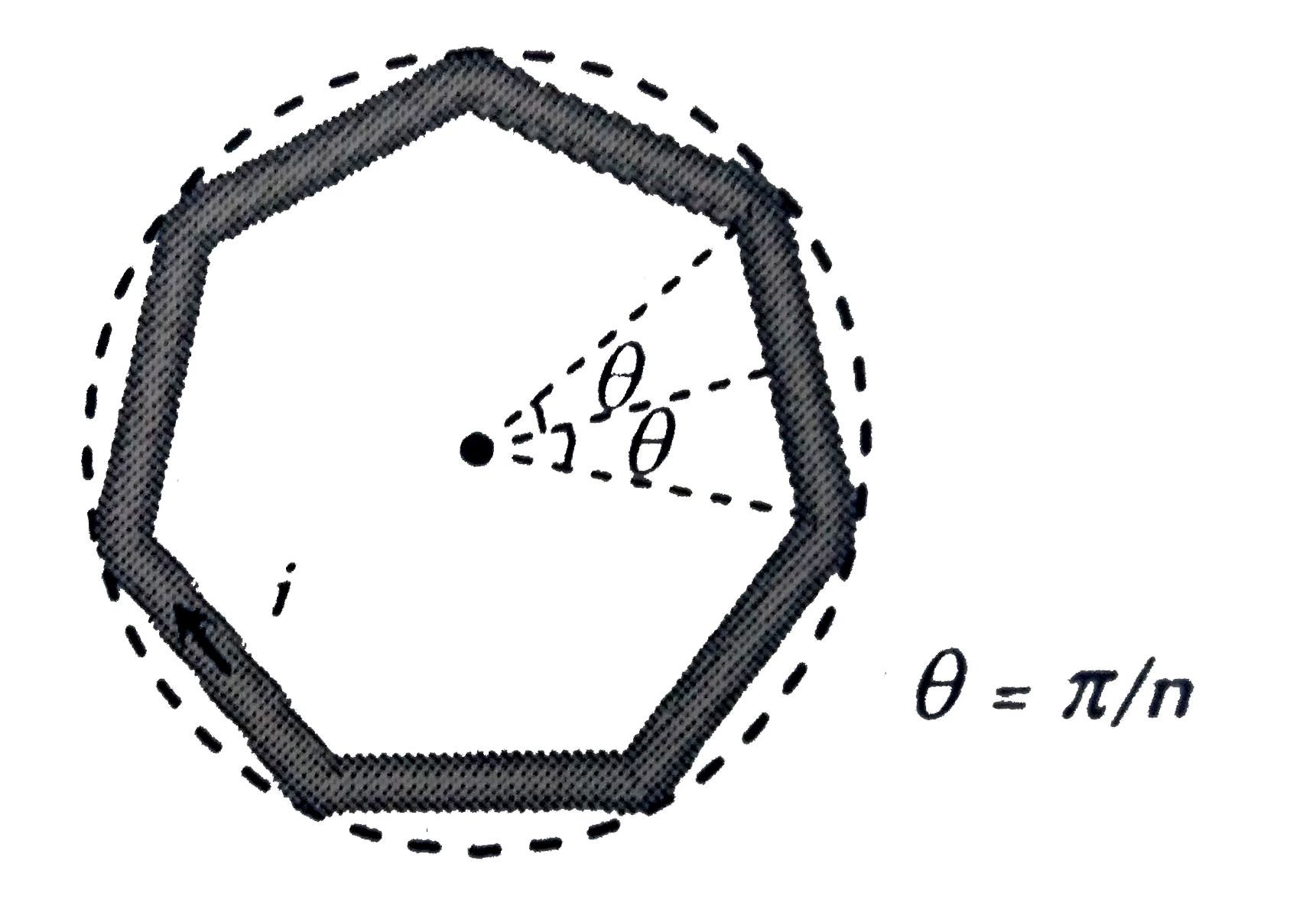
View SolutionLet An be the area that is outside a n-sided regular polygon and inside its circumscribeing circle. Also Bn is the area inside the polygon and outside the circle inscribed in the polygon. Let R be the radius of the circle circumscribing n-sided polygon. On the basis of above information, answer the equation If n=6 then An is equal to R2(π−√32) (b) R2(2π−6√32) R2(π−√3) (d) R2(2π−3√32)
View SolutionGiven that the area of a polygon of n sides circumscribed about a circle is to the area of the circumscribed polygon of 2n sides as 3:2 find n.
View SolutionA current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic field induction at the center of polygon due to one side of the polygon is
View SolutionA current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is
View SolutionA regular polygon of 10 sides is constructed. Triangles are formed joining vertices of the polygon. Find the number of triangles
(i) if two sides of trinangle coincide with the sides of polygon.
(ii) if only one side of triangle coincide with the side of polygon.
View SolutionThe sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
View Solution
