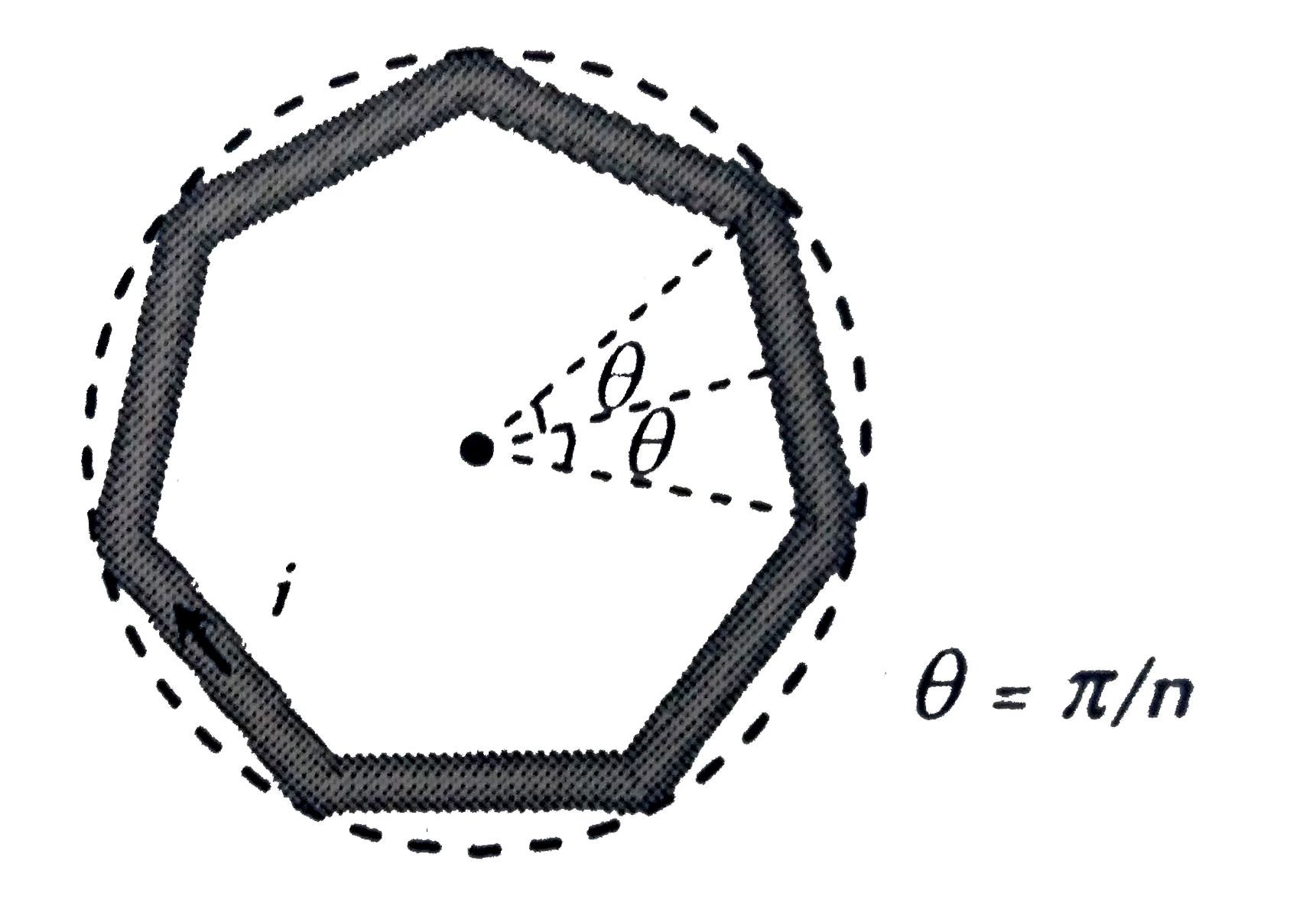
A current $I$ flows through a thin wire shaped as regular polygon of $n$ sides which can be inscribed in a circle of radius $R$ . The magnetic field induction at the center of polygon due to one side of the polygon is

$\frac{μ_{0} I}{π R} (\frac{tan π}{n})$

$\frac{μ_{0} I}{4 π R} (\frac{tan π}{n})$

$\frac{μ_{0} I}{2 π R} (\frac{tan π}{n})$

$\frac{μ_{0} I}{2 π R} (\frac{cos π}{n})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video & image solution for A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic field induction at the center of polygon due to one side of the polygon is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

A current $I$ flows through a thin wire shaped as regular polygon of $n$ sides which can be inscribed in a circle of radius $R$ . The magnetic field induction at the center of polygon due to one side of the polygon is

The correct Answer is:C

Similar Questions

Recommended Questions