A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is
μ0IπR(tanπn)
μ0I4πRtanπn
μ0I2πR(tanπn)
μ0I2πR(cosπn)
The correct Answer is:C
(c) B=μ0I4πr[2sinπn]

But cosπn=rRorr=Rcosπn
∴B=μ0I4πRcosπn[2sinπn]=μ0I2πr[tanπn]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )5videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )2videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )10videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
Similar Questions
A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic field induction at the center of polygon due to one side of the polygon is
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
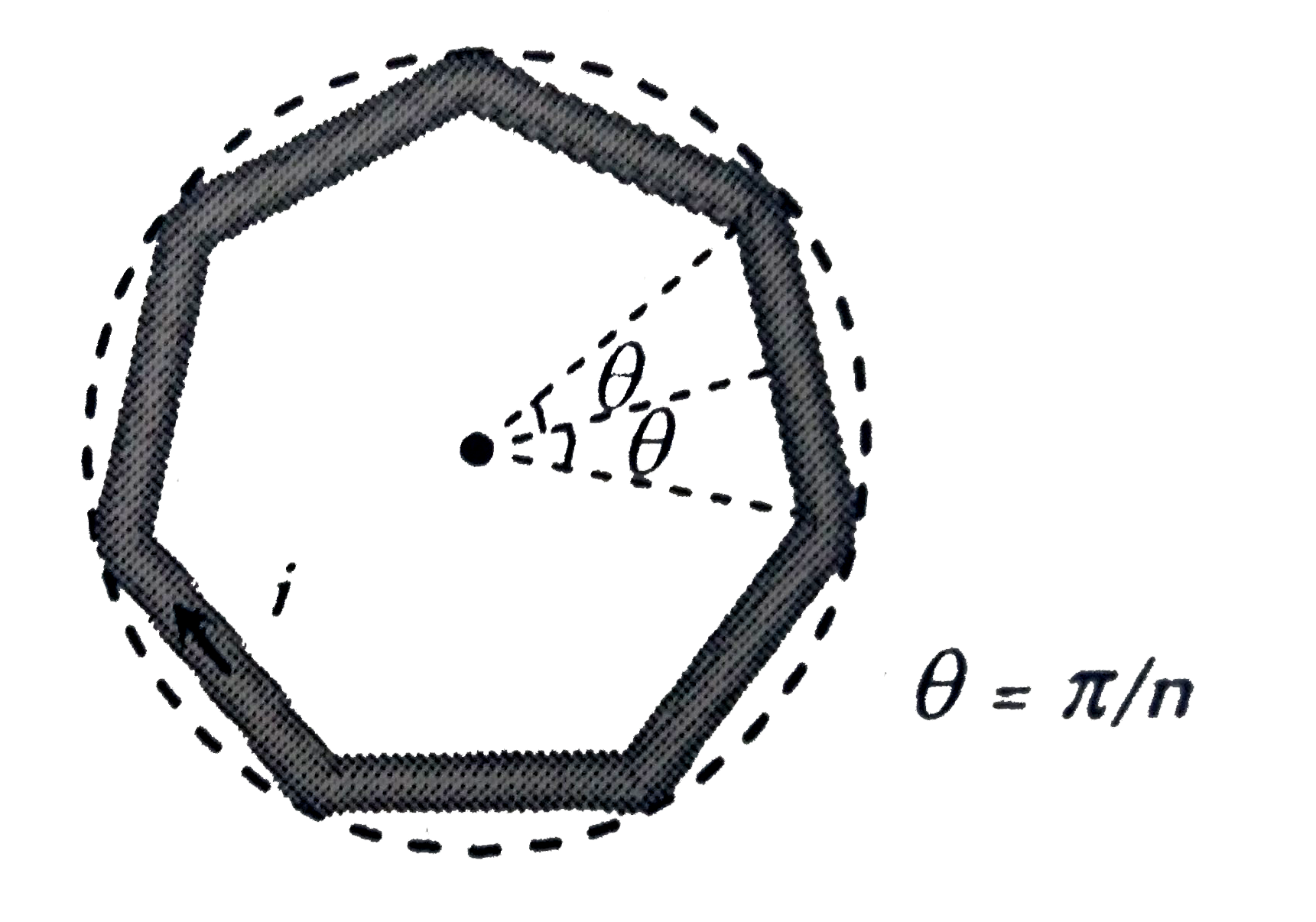 View Solution
View SolutionA current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when n→∞ is (R is the radius of its circumcircle)
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionCurrent 'i' is flowing in heaxagonal coil of side a. The magnetic induction at the centre of the coil will be
View SolutionIf a regular polygon of n sides has circum radius R and inradius r then each side of polygon is:
View SolutionIf r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
View SolutionProve that the area of a regular polygon hawing 2n sides, inscribed in a circle, is the geometric mean of the areas of the inscribed and circumscribed polygons of n sides.
View SolutionFind the radius of the circumscribing circle of a regular polygon of n sides each of length is a.
View Solution

