If A={a,b, c,d}, B={p,q,r,s} than Is the following relation from A → B? Give reasons for your answer.: R3={(a,p), (a,q), (d,p), (c,r), (b,r)}
To determine if the relation R3={(a,p),(a,q),(d,p),(c,r),(b,r)} is a relation from set A to set B, we need to check if all the first elements of the ordered pairs in R3 belong to set A and all the second elements belong to set B.
1. Identify the Sets:
- Set A={a,b,c,d}
- Set B={p,q,r,s}
2. List the Ordered Pairs in R3:
- The ordered pairs in the relation R3 are:
- (a,p)
- (a,q)
- (d,p)
- (c,r)
- (b,r)
3. Check the First Elements:
- The first elements of the ordered pairs are: a,a,d,c,b.
- All these elements (a,d,c,b) are present in set A.
4. Check the Second Elements:
- The second elements of the ordered pairs are: p,q,p,r,r.
- All these elements (p,q,r) are present in set B.
5. Conclusion:
- Since all first elements of the ordered pairs belong to set A and all second elements belong to set B, we conclude that R3 is indeed a relation from A to B.
Final Answer:
Yes, R3 is a relation from A to B because all first elements are from A and all second elements are from B.
- Set A={a,b,c,d}
- Set B={p,q,r,s}
- The ordered pairs in the relation R3 are:
- (a,p)
- (a,q)
- (d,p)
- (c,r)
- (b,r)
- The first elements of the ordered pairs are: a,a,d,c,b.
- All these elements (a,d,c,b) are present in set A.
- The second elements of the ordered pairs are: p,q,p,r,r.
- All these elements (p,q,r) are present in set B.
- Since all first elements of the ordered pairs belong to set A and all second elements belong to set B, we conclude that R3 is indeed a relation from A to B.
Yes, R3 is a relation from A to B because all first elements are from A and all second elements are from B.
Topper's Solved these Questions
Similar Questions
If A={a,b, c,d}, B={p,q,r,s} than is the following relation from A → B? Give reasons for your answer.: R1={(a,p), (b,r), (c,s)}
View SolutionIf A={a,b, c,d}, B={p,q,r,s} than Is the following relation from A → B? Give reasons for your answer.: R2={(q,b), (c,s), (d,r)}
View SolutionIf A={a,b, c,d}, B={p,q,r,s} than is the following relation from A → B? Give reasons for your answer.: R4={(a,p), (q,a), (b,s), (s,b)}
View SolutionLet A={p,q,r}. Which of the following is an equivalence relation on A? (a) R1={(p,q),(q,r),(p,r),(p,q)} (b) R2={(r,q),(r,p),(r.r),(q,r)} (c) R3={(p,p),(q,q),(r,r),(p,q)} (d) one of these
View SolutionMatch the columns and choose correct options.
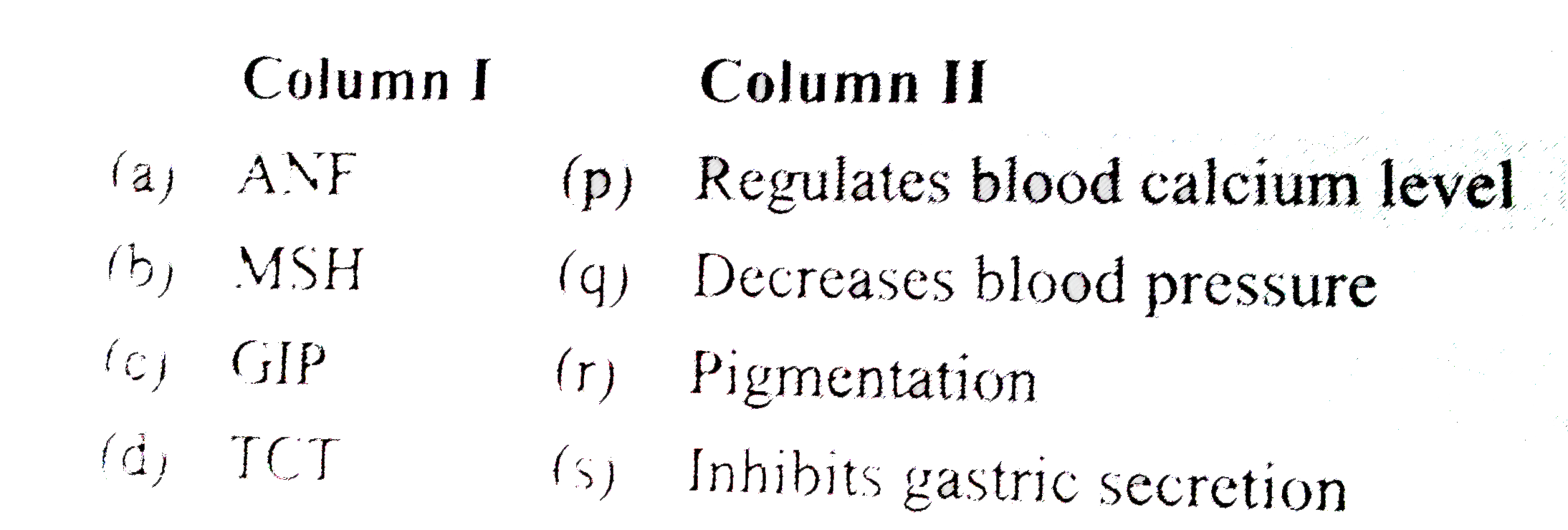
(1) a-q, b-r, c-s, d-p
(2) a-s, b-p, c-q, d-r
(3) a-q, b-p, c-s, d-r
(4) a-s, b-p, c-r, d-qView SolutionWhich of the following is not equivalent to (p∧~q)→r
(a) ~(qv~p)→r
(b) ~r→(~pvq)
(c)~((p∧(~q))∧(~r))
(d) ~r→(~p∧q)View SolutionIf q is false and (p∧q)↔r is also true then which of the following are tautology (A) (p∨r)→(p∧r) (B) (p∨r) (C) (p∧r)→(p∨r) (D) p∧r
View SolutionIf a, b, c are pth, qth and rth terms of a GP, the |logap1logbq1logcr1| is equal to- log abc b. 1 c.0 d. pqr
View SolutionIn Figure, PQ||AB and PR ||BC . If ∠QPR=1020 , determine ∠ABC. Give reasons.
View SolutionIn triangles ABC and PQR, if ∠A=∠R, ∠B=∠P and AB=RP , then which one of the following congruence conditions applies: SAS (b) ASA (c) SSS (d) RHS
View Solution

