If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar(△ABC):ar(△BDE)Solution in Punjabi
2:1
1:2
4:1
1:4
The correct Answer is:C
Step by step video, text & image solution for If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar(triangleABC) : ar(triangleBDE) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NAND LAL PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 6.514videos
TRIANGLES
- BOOK - NAND LAL PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 6.611videos
TRIANGLES
- BOOK - NAND LAL PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 6.323videos
TRIANGLES
- BOOK - NAND LAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUME EXERCISE - EXERCISE 13.57videos
SURFACE AREAS AND VOLUME
Similar Questions
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse. :- 7 cm, 24 cm, 25 cm
03:14View SolutionIn figure , D is point on hypotenuse AC of ΔABC,BD⊥AC,DM⊥BCandDN⊥AB. Prove that
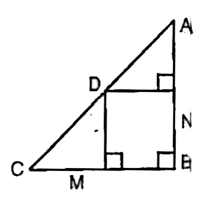
DM2=DN.MC19:27View SolutionState which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
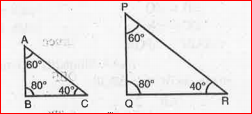 02:40View Solution
02:40View SolutionA copper wire 3 mm in diameter is wound about a cylinder whose length is 12 cm, and diameter 10 cm,so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to 8.88 g per cm3.
07:33View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
04:09View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
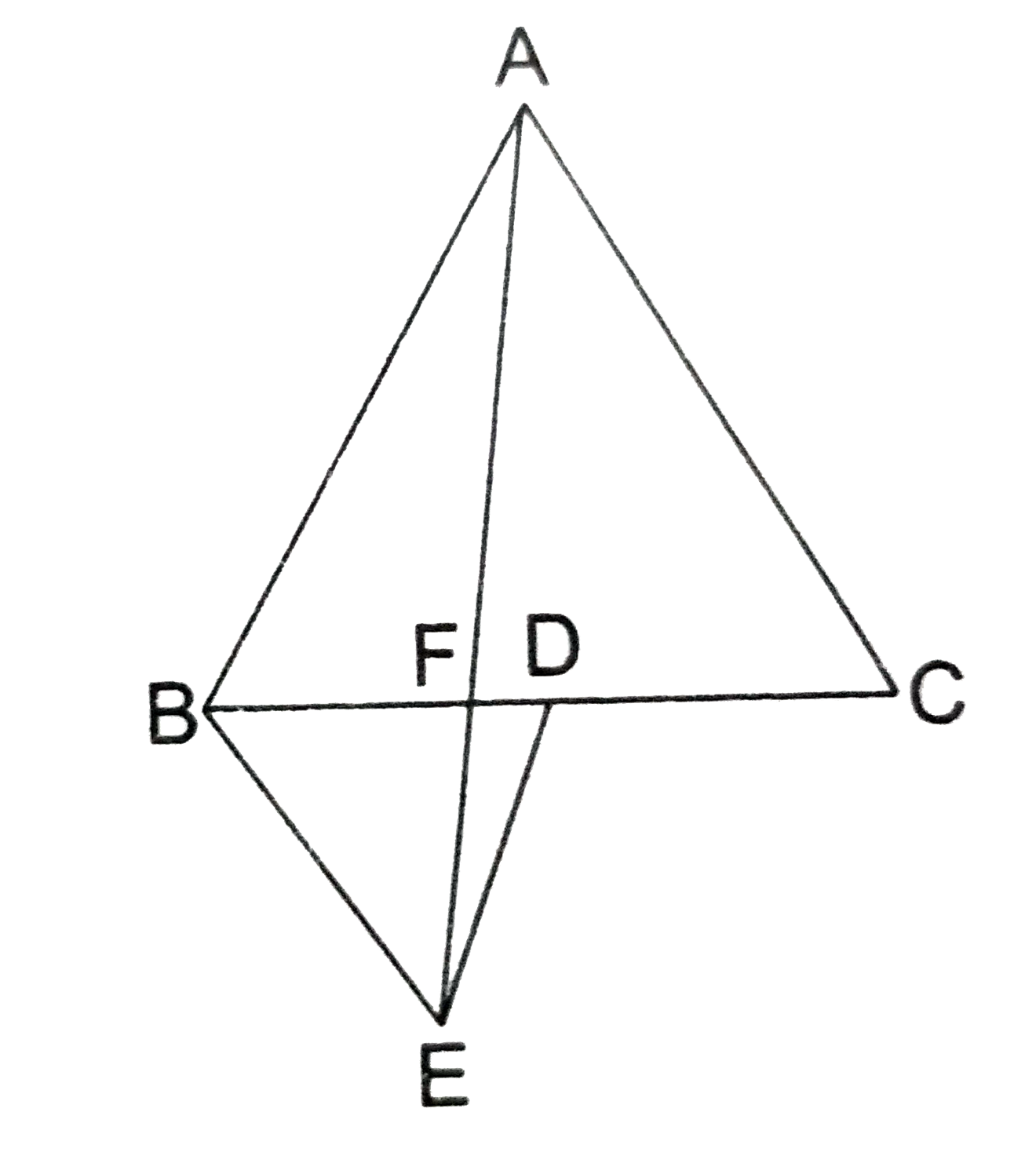 06:30View Solution
06:30View SolutionABC और BDE दो समबाहु त्रिभुज इस प्रकार है कि D भुजा BC का मध्य-बिंदु है त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात ज्ञात कीजिये
03:07View Solutionसत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए -
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब
ar(BDE)=14ar(ABC).02:12View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
02:36View SolutionIn fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
03:17View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
01:46View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
06:45View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/4 ar( Delta ABC)
02:37View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/2 ar( Delta BAE)
03:21View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta ABC) = 2 ar( Delta BEC)
04:16View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BFE) = 2 ar( Delta FED)
05:45View Solution

