If a,b,c ∈R, then for which of the following graphs of the quadratic polynomial y=ax2−2bx+c(a≠0), the product (abc) is negative ?
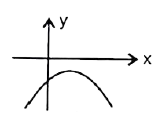
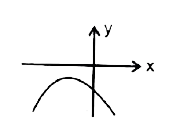

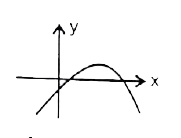
The correct Answer is:A, C, D
To solve the problem, we need to analyze the quadratic polynomial given by y=ax2−2bx+c where a,b,c∈R and a≠0. We want to determine for which of the given graphs the product abc is negative.
1. Identify the Sign of a:
- Since the problem states that the graphs are downward-opening parabolas, we know that a<0.
Hint: Remember that the direction of the parabola (upward or downward) is determined by the sign of a.
2. Determine Conditions for abc<0:
- For the product abc to be negative, given that a<0, it follows that bc must be positive (since a negative times a positive is negative).
Hint: If a is negative, then bc must be positive for the overall product abc to be negative.
3. Analyze Each Option:
- Option A:
- C (the value of the polynomial at x=0) is negative. Thus, c<0.
- The x-coordinate of the vertex −b2a>0, which implies b<0 (since a<0).
- Therefore, a<0, b<0, c<0 implies abc<0 is not satisfied (as bc>0).
- Conclusion: abc is positive, so this option is not correct.
Hint: Check the signs of b and c carefully based on the vertex condition.
- Option B:
- C is negative, so c<0.
- The x-coordinate of the vertex −b2a<0, which implies b>0 (since a<0).
- Thus, a<0, b>0, c<0 implies abc<0 is satisfied.
- Conclusion: This option is correct.
Hint: Ensure that the signs of b and c are consistent with the conditions given.
- Option C:
- C is positive, so c>0.
- The x-coordinate of the vertex −b2a<0, which implies b>0.
- Thus, a<0, b>0, c>0 implies abc>0.
- Conclusion: This option is not correct.
Hint: Remember that if c is positive, the product abc cannot be negative.
- Option D:
- C is negative, so c<0.
- The x-coordinate of the vertex −b2a>0, which implies b<0.
- Thus, a<0, b<0, c<0 implies abc<0 is not satisfied (as bc>0).
- Conclusion: This option is not correct.
Hint: Again, check the signs of b and c carefully.
Final Conclusion:
The only option for which the product abc is negative is Option B.
- Since the problem states that the graphs are downward-opening parabolas, we know that a<0.
- For the product abc to be negative, given that a<0, it follows that bc must be positive (since a negative times a positive is negative).
- Option A:
- C (the value of the polynomial at x=0) is negative. Thus, c<0.
- The x-coordinate of the vertex −b2a>0, which implies b<0 (since a<0).
- Therefore, a<0, b<0, c<0 implies abc<0 is not satisfied (as bc>0).
- Conclusion: abc is positive, so this option is not correct.
- C is negative, so c<0.
- The x-coordinate of the vertex −b2a<0, which implies b>0 (since a<0).
- Thus, a<0, b>0, c<0 implies abc<0 is satisfied.
- Conclusion: This option is correct.
- C is positive, so c>0.
- The x-coordinate of the vertex −b2a<0, which implies b>0.
- Thus, a<0, b>0, c>0 implies abc>0.
- Conclusion: This option is not correct.
- C is negative, so c<0.
- The x-coordinate of the vertex −b2a>0, which implies b<0.
- Thus, a<0, b<0, c<0 implies abc<0 is not satisfied (as bc>0).
- Conclusion: This option is not correct.
The only option for which the product abc is negative is Option B.
Topper's Solved these Questions
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)23videos
QUADRATIC EQUATIONS
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (MATCHING TYPE PROBLEMS)4videos
QUADRATIC EQUATIONS
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)45videos
QUADRATIC EQUATIONS
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - PROBABILITY EXERCISE - Exercise -5 : Subjective Type problems11videos
PROBABILITY
- BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)21videos
SEQUENCE AND SERIES
Similar Questions
For which of the following graphs the quadratic expression y=ax2+bx+c the product abc is negative ?
View SolutionThe graph of quadratic polynomical f(x)=ax2+bx+c is shown below
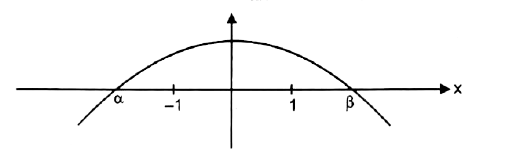 View Solution
View SolutionIf graph of the quadratic y=ax2+bx+c is given below :
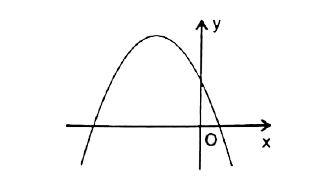 then: View Solution
then: View Solutionwhich of the following graph represents the expression f(x)=ax2+bx+c (a≠0) when a>0,b<0 $ c<0 ?
View SolutionThe quadratic expression ax2+bx+c>0∀x∈R, then :
View SolutionThe graph of a quadratic polynomial y=ax2+bx+c,a,b,εR is shown. Find its vertex,roots and D.
View SolutionIf the minimum value of the quadratic expression y=ax2+bx+c is negative attained at negative vlaue of x, then :
View SolutionLet a,b,c∈Q+ satisfying a>b>c. Which of the following statement(s) hold true of the quadratic polynomial f(x)=(a+b−2c)x2+(b+c−2a)x+(c+a−2b)? a. The mouth of the parabola y=f(x) opens upwards b. Both roots of the equation f(x)=0 are rational c. The x-coordinate of vertex of the graph is positive d. The product of the roots is always negative
View SolutionIf the graph of quadratic polynomial ax2+bx+c cuts negative direction of y-axis, then what is the sign of c ?
View SolutionThe discriminant of the quadratic equation ax2+bx+c=0is
View Solution

