If the graph of quadratic polynomial ax2+bx+c cuts negative direction of y-axis, then what is the sign of c ?
To determine the sign of c in the quadratic polynomial ax2+bx+c given that its graph cuts the negative direction of the y-axis, we can follow these steps:
Step 1: Understand the Graph's Intersection with the Y-Axis
The y-axis is where x=0. To find the point where the graph intersects the y-axis, we need to evaluate the polynomial at x=0.
Step 2: Evaluate the Polynomial at x=0
Substituting x=0 into the polynomial:
f(0)=a(0)2+b(0)+c=c
Thus, the intersection point on the y-axis is (0,c).
Step 3: Analyze the Given Condition
The problem states that the graph cuts the negative direction of the y-axis. This means that the value of c must be negative because the graph is below the x-axis at the point where it intersects the y-axis.
Step 4: Conclusion
Since the graph cuts the negative direction of the y-axis, we conclude that:
c<0
Final Answer
The sign of c is negative, or mathematically:
c<0
---
The y-axis is where x=0. To find the point where the graph intersects the y-axis, we need to evaluate the polynomial at x=0.
Substituting x=0 into the polynomial:
f(0)=a(0)2+b(0)+c=c
Thus, the intersection point on the y-axis is (0,c).
The problem states that the graph cuts the negative direction of the y-axis. This means that the value of c must be negative because the graph is below the x-axis at the point where it intersects the y-axis.
Since the graph cuts the negative direction of the y-axis, we conclude that:
c<0
The sign of c is negative, or mathematically:
c<0
Topper's Solved these Questions
Similar Questions
If graph of quadratic polynomial ax2+bx+c cuts positive direction of y-axis, then what is the sign of c ?
View SolutionDraw the graph of the quadratic polynomial f(x)=3−2x−x2
View SolutionIf one of the zeroes of a quadratic polynomial of the form x2+ax+b is the negative of the other, then it
View SolutionIf one zero of the quadratic polynomial f(x)=4x2−8kx−9 is negative of the other, find the value of k .
View SolutionThe graph of a quadratic polynomial y=ax2+bx+c,a,b,εR is shown. Find its vertex,roots and D.
View SolutionIf graph of the quadratic y=ax2+bx+c is given below :
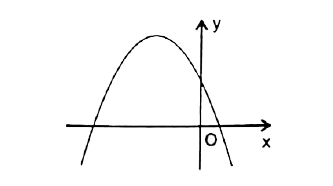 then:
then:
View SolutionIf a,b,c ∈R, then for which of the following graphs of the quadratic polynomial y=ax2−2bx+c(a≠0), the product (abc) is negative ?
View SolutionIf the zeroes of the quadratic polynomial x2+(a+1)x+b are 2 and -3, then: a and b are
View SolutionThe graph of the quadratic trinomial u=ax2+bx+c has its vertex at (4, -5) and two x-intercepts, one positive and one negative. Which of the following holds good? a. a>0 b. b<0 c. c<0 d. 8a=b
View SolutionFind the equation of a line which cuts an intercept of 5 units from negative direction of Y-axis and makes an angle of 1350 from the positive direction of X-axis.
View Solution
