If AD is median of ΔABC and P is a point on AC such that ar(ΔADP):ar(ΔABD)=4:5 then ar(ΔPDC):ar(ΔABC) is
1:10
10:1
1:3
3:1
The correct Answer is:A
Step by step video, text & image solution for If AD is median of DeltaABC and P is a point on AC such that ar(DeltaADP):ar(DeltaABD)=4:5 then ar(DeltaPDC):ar(DeltaABC) is by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
AD is one of the medians of a ABC..X is any point on AD . Show that ar(ABX)=ar(ACX)
View SolutionIn △ABC ,AD is a median and P is a point on AD such that AP : PD = 3 : 4. Then ar(△BPD):ar(△ABC) is equal to:
त्रिभुज ABC में, AD एक माध्यिका है और P, AB पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है| ar(△BPD):ar(△ABC) ज्ञात करें |View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, AD is the median and E is any point on AC, such that ar(ΔMDE) : ar(ΔABD) = 2 : 3, then find the ratio of ar(ΔEDC): ar(ΔABC).
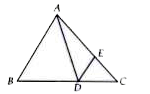 A3 : 4B1 : 6C6 : 1D4 : 3
A3 : 4B1 : 6C6 : 1D4 : 3 - Question 2 - Select One
In ΔABC,AD is the bisector of ∠A . Then , ar(ΔABD)ar(ΔACD)=
AAB2AC2BABACCBMCMDNone of these - Question 3 - Select One
In ΔABC, P is a point on BC such that BP : PC = 2 : 3 and Q is the midpoint of BP. Then ar (ΔABQ):ar(ΔABC) is equal to :
A1:4B2:5C1:5D2:3
In △ABC, AD is median and P is the point on AD such that AP : PD = 3 : 4, then ar(△APB):ar(△ABC) is equal to :
त्रिभुज ABC में, AD मध्यिका है तथा P, AD पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है, तो ar(△APB):ar(△ABC) का मान किसके बराबर होगा ?View SolutionIf ΔABC and ΔDEF are two tnangles such that ABEF=BCFD=CADE=34 then find ar(ΔDEF):ar(ΔABC).
View SolutionA point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)
 View Solution
View SolutionIn the ΔABC , MN||BC and AM : : MB = 13.
Then, ar(ΔAMN)ar(ΔABC)=?View Solution

