If an=34−(34)2+(34)3+...(−1)n−1(34)n and bn=1−an, then find the minimum natural number n, such that bn>an
A
5
B
6
C
7
D
none of these
Video Solution
Text Solution
The correct Answer is:B
We have
An=34−(34)2+(34)3+....+(−1)n−1(34)n
⇒ An=−(−34)−(−34)−(−34)3+....+(−)n(−34)n
⇒ An=−⎡⎢
⎢
⎢⎣(−34)⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩1−(−34)41−(−34)⎫⎪
⎪
⎪⎬⎪
⎪
⎪⎭⎤⎥
⎥
⎥⎦=37{1−(−34)n}
Now,
⇒ Bn>An
⇒ 1−An>An [∵Bn=1−An]
⇒ An<12
⇒ 37{1−(−34)n}<12
⇒ 1−(−34)n<76⇒(−34)n>−16
Clearly, it is true for all even natural numbers.
If n is odd natural number, then
(−34)n>−16⇒−6×3n>−4n⇒3n+1<22n−1
This is true for all n<7. Hence, n0=7.
|
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Section II - Assertion Reason Type
13 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise
129 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
60 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test
50 Videos
- SETSBOOK - OBJECTIVE RD SHARMACHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
IF an=1n+1+1 then find the value of a1+a3+a5
A1712B2712C3712D4712If 1.3+2.32+3.33+...=n3n=(2n−1)3+b4, then a and b are respectively:
An,2Bn,3Cn+1,2Dn+1,3
Let An=34−(34)2+(34)3−...+(−1)n−1(34)nandBn=1−An, then find the least value of n0,n0∈N such that Bn>An,∀n≥n0.
View SolutionComplete the following statements.
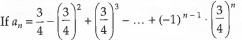 and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
View Solution13+23+33+.....+n3=n(n+1)24,n∈N
View Solution1+5+9+...+(4n−3)=n(2n−1) for all natural numbers n
View SolutionIn an AP, given an=4,d=2,Sn=−14 find n and a
View Solution∞∑n=1(14n−3−14n−1)=πn find n
View Solution
