If $a x^{2} + b x + c = 0$ have two distinct roots lying int eh interval $(0, 1), a, b, c e π s l o n N$
The least value of $a$ is Solution in Bengali

A

4

B

6

C

7

D

5

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

$a z^{2} - b x + c = 0$
Let $f (x) = a x^{2} - b x + c$ be
the correspoding quadratic expression and $α, β$ be the roots of $f (x) = 0$ .

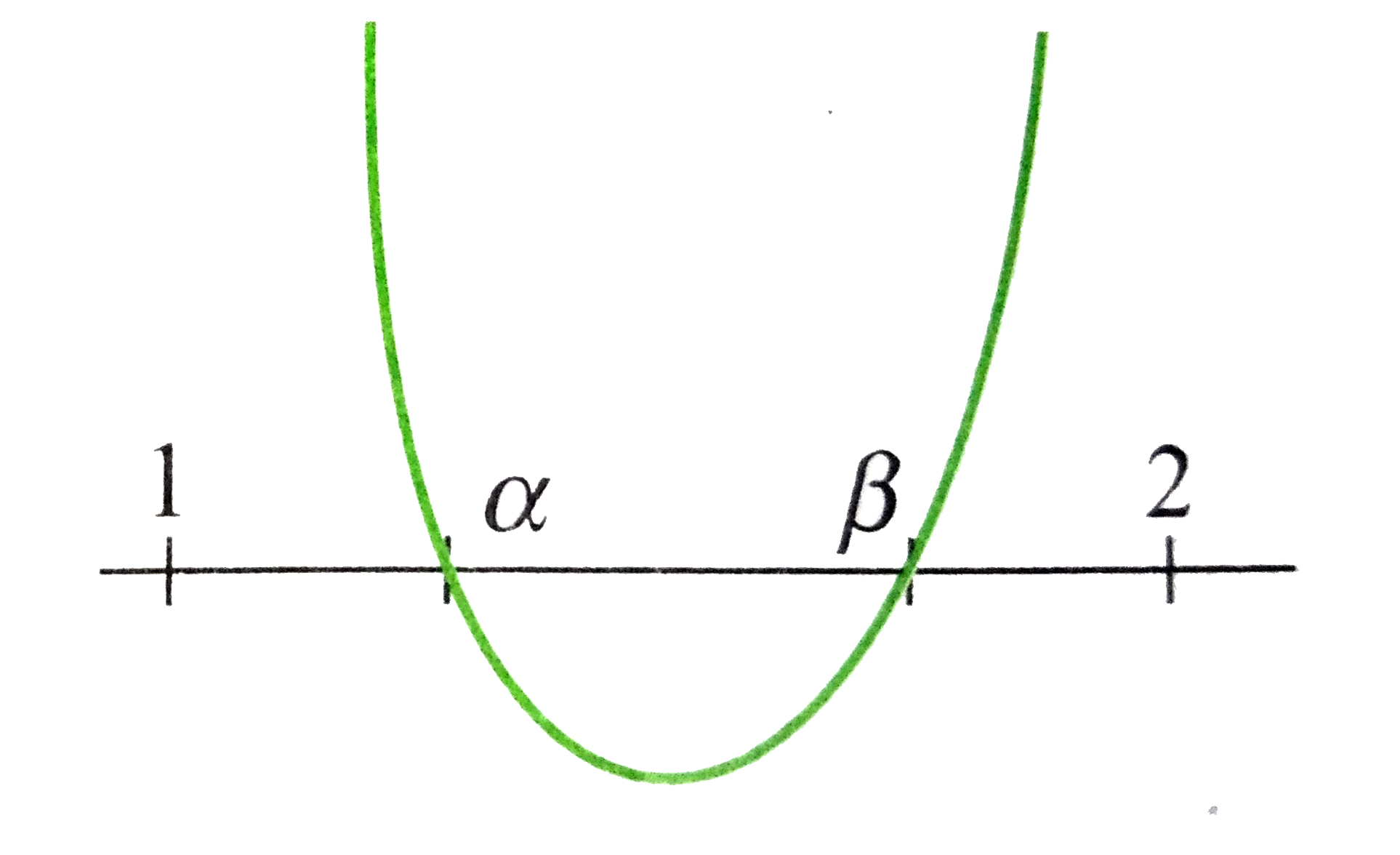
Then, $f (x) = a (x - α) (x - β)$
Now, $a f (1) > 0, a f (2) > 0, 1 < \frac{b}{2 a} < 2, b^{2} - 4 a c > 0$
$\Rightarrow a (1 - α) (1 - β) > 0, a (2 - α) (2 - β) > 0, 2 a < b < 4 a, b^{2} - 4 a x > 0$
$\Rightarrow a^{2} (1 - α) (1 - β) (2 - α) (2 - β) > 0$
$\Rightarrow a^{2} (1 - α) (1 - β) (2 - α) (2 - β) > 0$
As $f (x)$ and $f (2)$ both are integers and $f (1) > 0$ , and $f (2) > 0$ , so
$f (1) f (2) > 0$
$\Rightarrow f (1) f (2) > 1$
$\Rightarrow 1 \geq a^{2} (α - 1) (2 - α) (β - 1) (2 - β) (1)$
Now, $\frac{(α - 1) + (2 - α)}{2} > {((α - 1) (2 - α))}^{1 / 2}$
$\Rightarrow (α - 1) (2 - α) \leq \frac{1}{4}$
Similarly,
$(β - 1) (2 - β) \leq \frac{1}{4}$
$\Rightarrow (α - 1) (2 - α) (β - 1) (2 - β) < \frac{1}{16}$
As $α \neq β$ , so $α^{2} > 1 (Using (1))$
$\Rightarrow a > 5$
$\Rightarrow b^{2} > 20 c and b > 10 \Rightarrow b \geq 11$
Also, $b^{2} > 100 \Rightarrow c > 5 \Rightarrow c \geq 6$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-THEORY OF EQUATIONS-Linked Comprechension Type

Home
Ask Doubt
Profile