If cosθ=35,find the value of (5cosec θ−4tanθsecθ+cotθ).
A
2429
B
129
C
829
D
1129
Video Solution
Text Solution
The correct Answer is:D
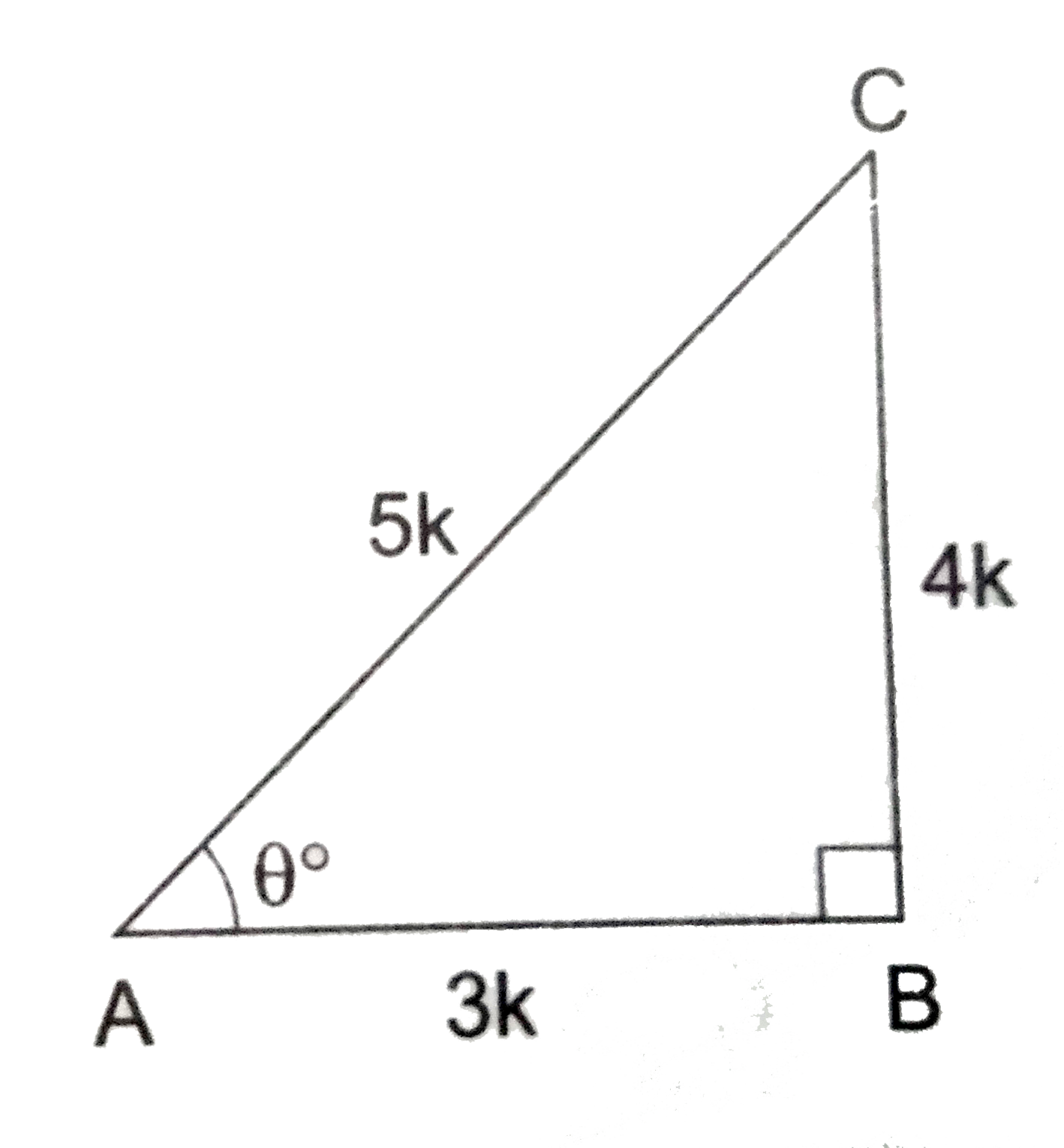
Let us draw a ΔABCin which ∠B=90∘.
Let ∠A=θ∘.
then ,cosθ=ABAC=35.
Let AB=3KandAc=5k , where k is positive .
By pythagoras' theorem , we have
AC2=AB2+BC2
⇒BC2=AC2−AB2=(5k)2−(3k)2=25k2−9k2=16k2
⇒BC=√16k2=4k.
∴secθ=1cosθ=53,tanθ=BCAB=4k3k=43,
cotθ=1tanθ=34,andcosec θ=ACBC=5k4k=54.
∴(5cosec θ−4tanθsecθ+cotθ)=(5×54−4×43)(53+34)=(254−163)(53+34)
=75−641220+912=(1112×1229)=1129.
|
Topper's Solved these Questions
- TRIGONOMETRIC RATIOSBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 10
35 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 12
15 Videos
Similar Questions
Knowledge Check
If secθ=54,find the value of (2cosθ−sinθ)(cotθ−tanθ)=.
A(12)/(7)B(12)/(5)C(1)/(7)D(2)/(5)If 5cotθ=3, find the value of (5sinθ−3cosθ4sinθ+3cosθ).
A1129B1619C1629D3429If cosθ=−35andπ<θ<3π2, then find the value of secθ−tanθcosecθ+cotθ is-
A6B8C−2D−4
If cosθ=35, then find the value of tanθ,cosecθ
View SolutionIf 3cotθ=4, find the value of 5sinθ−3cosθ5sinθ+3cosθ.
View SolutionIf cosθ=45 , then value of cosecθ1+cotθ is
View SolutionIf cosecθ=√5/2, find the value of secθ+tanθ−cotθ.
View SolutionIf secθ−tanθsecθ+tanθ=35,then the value of cosecθ+cotθcosecθ−cotθ is:
View Solution
