If cosθ=817,verify that 3−4sin2θ4cos2θ−3=3−tan2θ1−3tan2θ.
Video Solution
Text Solution
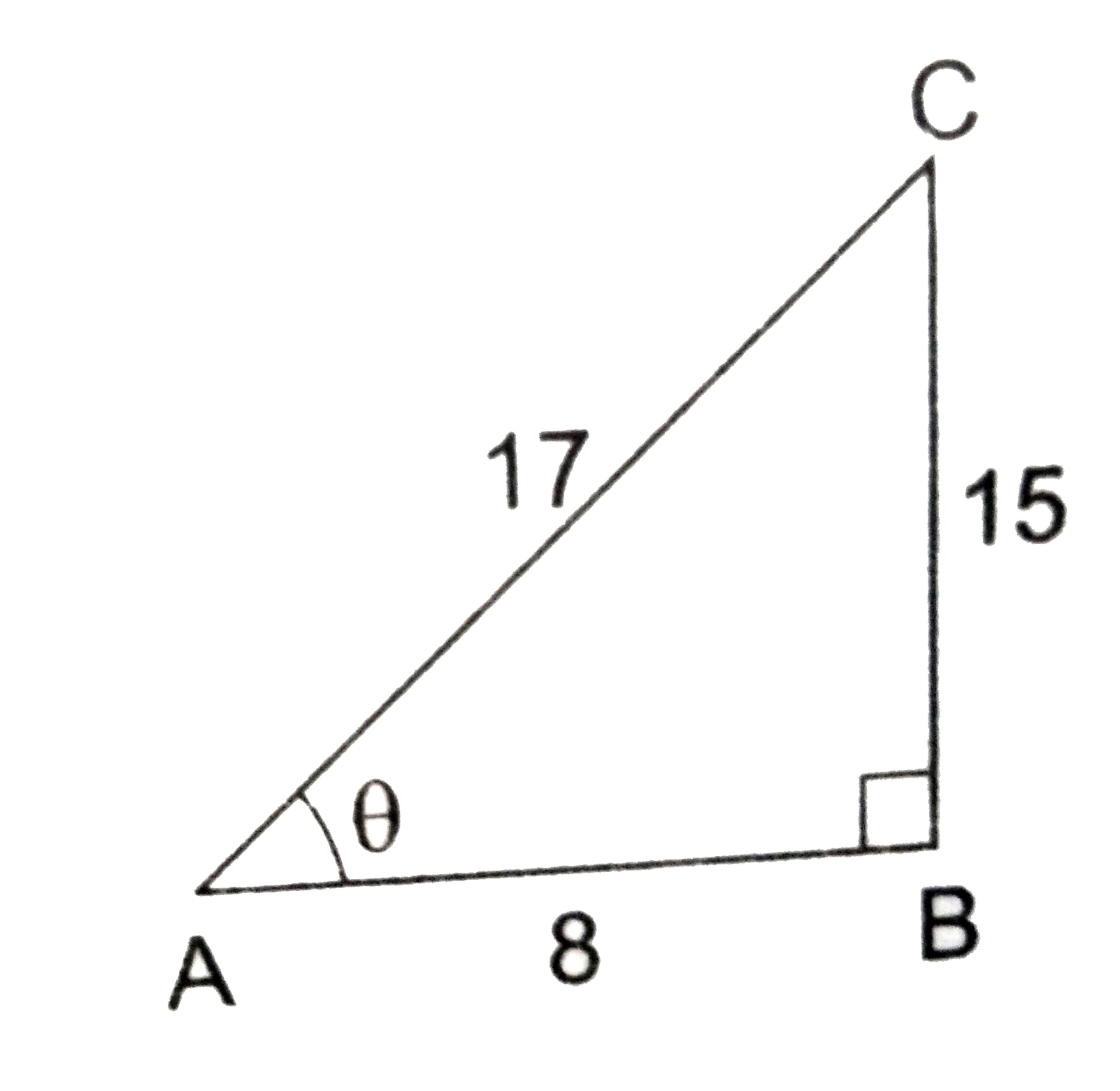
secθ=178⇒cosθ=817=ABAC.
∴BC2=AC2−AB2=(17)2−(8)2=(289−64)=225
⇒BC=√225=15.
∴sinθ=1517,cosθ=817andtanθ=158.
then ,LHS =RHS =3611.
|
Topper's Solved these Questions
- TRIGONOMETRIC RATIOSBook:RS AGGARWALChapter:TRIGONOMETRIC RATIOSExercise:Exercise 10
Explore 35 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES Book:RS AGGARWALChapter:TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES Exercise:Exercise 12
Explore 15 Videos
Similar Questions
Knowledge Check
3−4sin2θcos2θ+tan2θ is :
A1B2C3Dnone of these
If tanθ=34, then 4sin2θ−2cos2θ4sin2θ+3cos2θ
View SolutionIf tanθ=34, then 4sin2θ−2cos2θ4sin2θ+3cos2θ
View SolutionProve that :
sinθ−2sin3θ2cos3θ−cosθ=tanθ.
View SolutionIf 3cotθ=4 then show that 1−tan2θ1+tan2θ=(cos2θ−sin2θ)
View SolutionIf θ=30∘ , verify that: (i) cos2θ=1−tan2θ1+tan2θ (ii) cos3θ=4cos3θ−3cosθ
View SolutionProve that :tan4θ=4tanθ−4tan3θ1−6tan2θ+tan4θ.
View SolutionIf 3cosθ=1 , find the value of 6sin2θ+tan2θ4cosθ
View Solution