If ΔABC≅ΔPRQ, then ∠BandPQ are respectively equal to
∠PandAC
∠RandBC
∠RandAC
∠QandAB
The correct Answer is:C
To solve the problem, we need to use the concept of congruence of triangles. Given that triangle ABC is congruent to triangle PRQ (denoted as ΔABC ≅ ΔPRQ), we can conclude that their corresponding parts are equal.
1. Understanding Congruence:
Since ΔABC ≅ ΔPRQ, it means that all corresponding sides and angles of these triangles are equal.
2. Identifying Corresponding Parts:
From the congruence, we can identify the corresponding parts:
- Side AB corresponds to side PR.
- Side BC corresponds to side RQ.
- Side AC corresponds to side PQ.
- Angle A corresponds to angle P.
- Angle B corresponds to angle R.
- Angle C corresponds to angle Q.
3. Using CPCT:
The acronym CPCT stands for "Corresponding Parts of Congruent Triangles". This means:
- AB = PR
- BC = RQ
- AC = PQ
- Angle A = Angle P
- Angle B = Angle R
- Angle C = Angle Q
4. Finding the Required Angles and Sides:
We need to find the measures of angle B and side PQ:
- From CPCT, we know that angle B = angle R.
- Also, from CPCT, we know that side PQ = side AC.
5. Conclusion:
Therefore, angle B is equal to angle R, and side PQ is equal to side AC.
Final Answer:
- Angle B = Angle R
- Side PQ = Side AC
Since ΔABC ≅ ΔPRQ, it means that all corresponding sides and angles of these triangles are equal.
From the congruence, we can identify the corresponding parts:
- Side AB corresponds to side PR.
- Side BC corresponds to side RQ.
- Side AC corresponds to side PQ.
- Angle A corresponds to angle P.
- Angle B corresponds to angle R.
- Angle C corresponds to angle Q.
The acronym CPCT stands for "Corresponding Parts of Congruent Triangles". This means:
- AB = PR
- BC = RQ
- AC = PQ
- Angle A = Angle P
- Angle B = Angle R
- Angle C = Angle Q
We need to find the measures of angle B and side PQ:
- From CPCT, we know that angle B = angle R.
- Also, from CPCT, we know that side PQ = side AC.
Therefore, angle B is equal to angle R, and side PQ is equal to side AC.
- Angle B = Angle R
- Side PQ = Side AC
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Match the following
2 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Assertion & Reaction Type
5 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - NCERT Section (Exercise 7.2)
20 Videos
- COMPARING QUANTITIES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner
20 Videos
- DATA HANDLINGBOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner
20 Videos
Similar Questions
Knowledge Check
If O is the circumcentre of ΔABC and OD ⊥ BC, then ∠BOD must be equal to
A∠AB12∠AC12∠BD12∠CIn ΔABC, D and E are points on AB and AC respectively such that DE||BC and DE divides the ΔABC into two parts of equal areas. Then ratio of AD and BD is
A1:1B1:√2−1C1:√2D1:√2+1If D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
A6, 8 and 20 cmB4, 6 and 8 cmC5, 6 and 8 cmD103, 9 and 12 cm
If ΔABC~ΔZYX, then name the angles equal to ΔB and ΔZ respectively.
View SolutionThe heights of ΔABC and ΔDBC are 4 cm and 6 cm respectively. Find A(ΔABC)A(ΔDBC).
View SolutionIn ΔABC, D and E are points on AB and AC respectively such that DE is parallel to BC. If AD= 2 cm, BD = 3 cm, then ar(ΔADE)ar(ΔABC) is
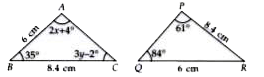
View SolutionFind the value of x and y respectively, if ΔABC≅ΔQRP.
View SolutionΔABCandΔDEF are two similar triangle and the primeters of ΔABCandΔDEF are 30 cm and 18 cm respectively . If the length of DE = 36 cm , then length of AB is
View Solution
